力扣第 102 场双周赛

比赛时间 2023-04-15。本场周赛国服共 884 人 AK。

T1. 查询网格图中每一列的宽度（3 分）

解题思路

模拟。

时间复杂度：O(mnlogU)。其中 U 表示最大值 1e9。

参考代码

class Solution {
    public int[] findColumnWidth(int[][] grid) {
        int n = grid[0].length;

        int[] res = new int[n];
        for (int j = 0; j < n; j++) {
            int max = 0;
            for (int[] ints : grid) {
                int len = String.valueOf(ints[j]).length();
                max = Math.max(max, len);
            }
            res[j] = max;
        }
        return res;
    }
}

T2. 一个数组所有前缀的分数（4 分）

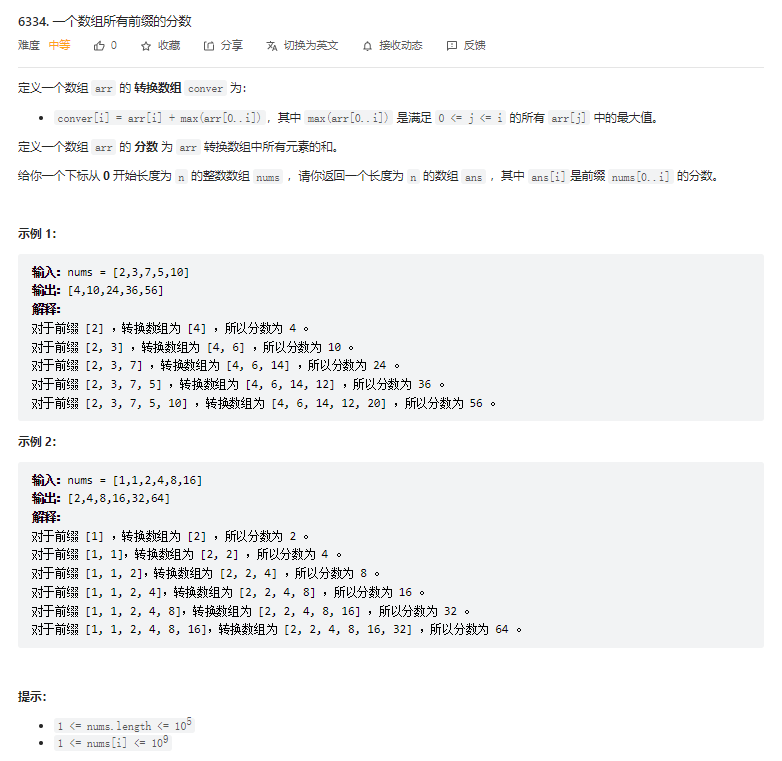
解题思路

模拟。

时间复杂度：O(n)。

参考代码

class Solution {
    public long[] findPrefixScore(int[] nums) {
        int n = nums.length;
        long[] conver = getConver(nums, n);

        long[] res = new long[n];
        res[0] = conver[0];
        for (int i = 1; i < n; i++) {
            res[i] = res[i - 1] + conver[i];
        }
        return res;
    }

    private long[] getConver(int[] nums, int n) {
        long[] conver = new long[n];
        int max = 0;
        for (int i = 0; i < n; i++) {
            max = Math.max(max, nums[i]);
            conver[i] = max + nums[i];
        }
        return conver;
    }
}

T3. 二叉树的堂兄弟节点 II（4 分）

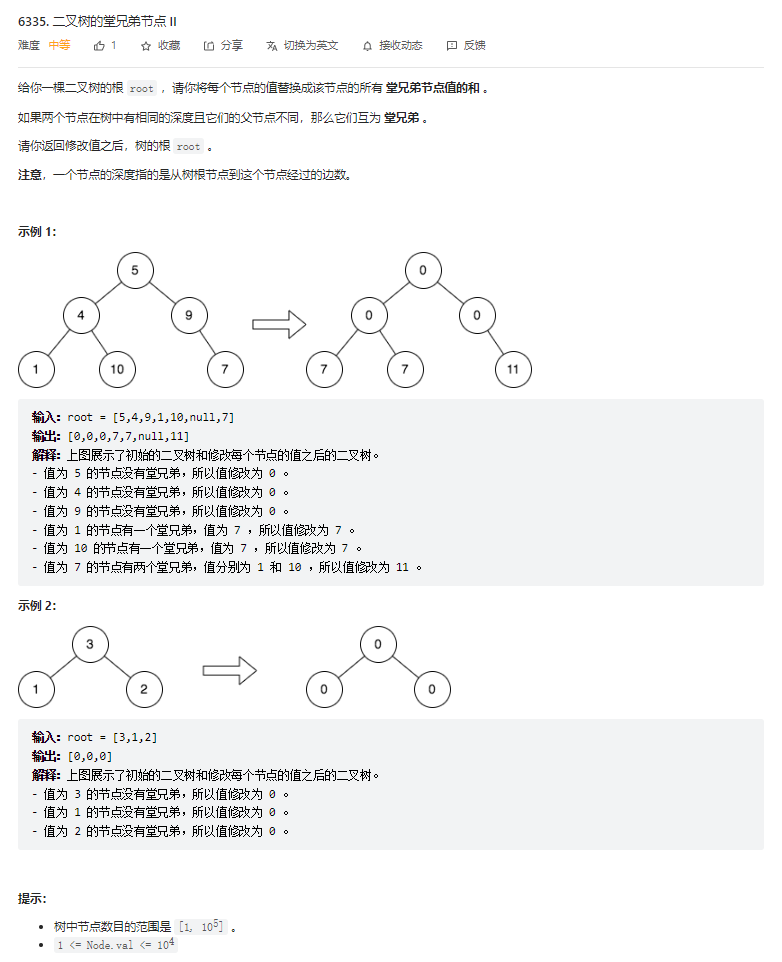
解题思路

层序遍历（双数组 BFS）。先算出下一层的和，再减去堂兄弟节点的和。

时间复杂度：O(n)。

参考代码

class Solution {
    public TreeNode replaceValueInTree(TreeNode root) {
        root.val = 0;

        // 双数组 BFS
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            Queue<TreeNode> tmp = new ArrayDeque<>(queue);
            queue.clear();

            // 求下一层的和
            int nextLevelSum = 0;
            for (TreeNode node : tmp) {
                if (node.left != null) {
                    nextLevelSum += node.left.val;
                    queue.add(node.left);
                }
                if (node.right != null) {
                    nextLevelSum += node.right.val;
                    queue.add(node.right);
                }
            }

            for (TreeNode node : tmp) {
                // 求堂兄弟节点的和
                int botherSum = (node.left == null ? 0 : node.left.val)
                        + (node.right == null ? 0 : node.right.val);
                if (node.left != null) {
                    node.left.val = nextLevelSum - botherSum;
                }
                if (node.right != null) {
                    node.right.val = nextLevelSum - botherSum;
                }
            }
        }
        return root;
    }
}

T4. 设计可以求最短路径的图类（5 分）

解题思路

最短路。

如果题目调整为调用 addEdge 至多 100 次。调用 shortestPath 至多 1e5 次。将是道好题。查多改少场景需要用到 Floyd。

比赛时使用了 dijkstra 堆优化模板。

时间复杂度：O(qmlogn)。

参考代码

Dijkstra 最短路：

class Graph {
    private final int n;
    private static final int INF = Integer.MAX_VALUE;
    private final int[][] adj;

    public Graph(int n, int[][] edges) {
        this.n = n;
        adj = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                adj[i][j] = (i == j) ? 0 : INF;
            }
        }
        for (int[] edge : edges) {
            adj[edge[0]][edge[1]] = edge[2];
        }
    }

    public void addEdge(int[] edge) {
        adj[edge[0]][edge[1]] = edge[2];
    }

    public int shortestPath(int node1, int node2) {
        int[] dist = dijkstra(node1);
        return dist[node2] == INF ? -1 : dist[node2];
    }

    private int[] dijkstra(int node1) {
        int[] dist = new int[n];
        boolean[] visited = new boolean[n];
        Arrays.fill(dist, INF);
        PriorityQueue<int[]> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(o -> o[1]));
        priorityQueue.add(new int[]{node1, 0});
        dist[node1] = 0;
        while (!priorityQueue.isEmpty()) {
            int[] top = priorityQueue.remove();
            int x = top[0];
            if (visited[x]) {
                continue;
            }
            visited[x] = true;
            for (int y = 0; y < n; y++) {
                if (x != y && adj[x][y] != INF) {
                    if (dist[y] > dist[x] + adj[x][y]) {
                        dist[y] = dist[x] + adj[x][y];
                        priorityQueue.add(new int[]{y, dist[y]});
                    }
                }
            }
        }
        return dist;
    }
}

Floyd 最短路：

class Graph {
    private final int n;
    private static final int INF = (int) 1e9;
    private final int[][] adj;

    public Graph(int n, int[][] edges) {
        this.n = n;
        adj = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                adj[i][j] = (i == j) ? 0 : INF;
            }
        }
        for (int[] edge : edges) {
            adj[edge[0]][edge[1]] = edge[2];
        }
        // Floyd 初始化 时间复杂度 O(n^3)
        // 定义 f[k][i][j] 表示除了 i 和 j 以外，从 i 到 j 的路径中间点上至多为 k 的时候
        // 从 i 到 j 的最短路的长度
        // 分类讨论：
        // 从 i 到 j 的最短路中间至多为 k-1
        // 从 i 到 j 的最短路中间至多为 k：说明 k 一定是中间节点
        // f[k][i][j] = min(f[k-1][i][j], f[k-1][i][k] + f[k-1][k][j])
        // 空间压缩 f[i][j] = min(f[i][j], f[i][k] + f[k][j])
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    adj[i][j] = Math.min(adj[i][j], adj[i][k] + adj[k][j]);
                }
            }
        }
    }

    // 新增边 时间复杂度 O(n^2)
    public void addEdge(int[] edge) {
        int u = edge[0], v = edge[1], w = edge[2];
        // 无效更新
        if (w > adj[u][v]) {
            return;
        }
        adj[u][v] = w;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                adj[i][j] = Math.min(adj[i][j], adj[i][u] + adj[u][v] + adj[v][j]);
            }
        }
    }

    public int shortestPath(int node1, int node2) {
        return adj[node1][node2] == INF ? -1 : adj[node1][node2];
    }
}

（全文完）