力扣第 105 场双周赛

比赛时间 2023-05-27。本场周赛国服共 413 人 AK。

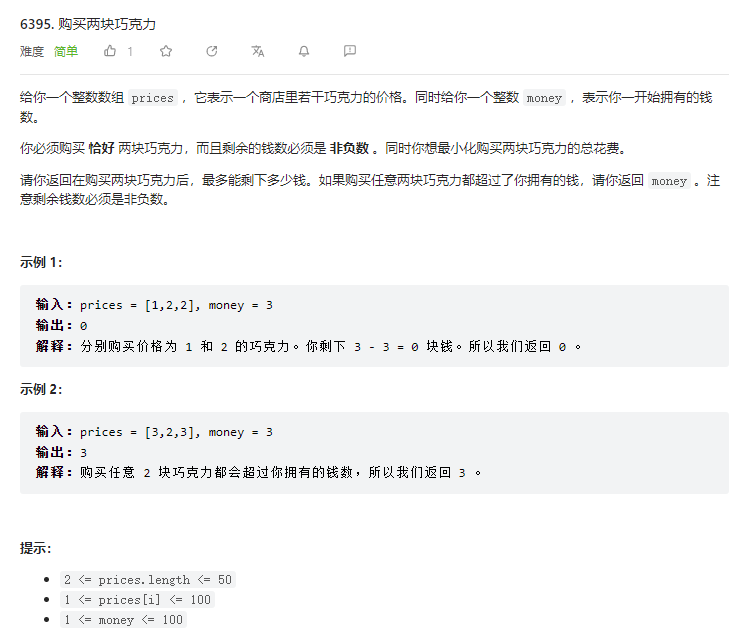
T1. 购买两块巧克力（3 分）

解题思路

贪心。

时间复杂度：O(nlogn)。也可以不使用排序优化至 O(n)。

参考代码

class Solution {
    public int buyChoco(int[] prices, int money) {
        Arrays.sort(prices);
        int ans = money - prices[0] - prices[1];
        return ans >= 0 ? ans : money;
    }
}

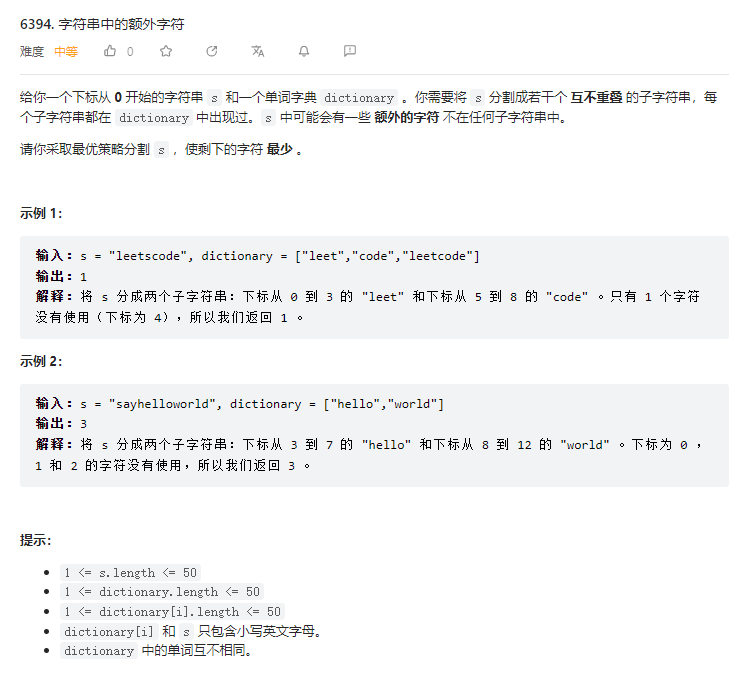
T2. 字符串中的额外字符（4 分）

解题思路

记忆化搜索。

时间复杂度：O(L + n^3)。其中 L 为 dictionary 所有字符串的长度之和。

参考代码

class Solution {
    private int n;
    private Map<Integer, List<Integer>> lrs;
    private int[] memo;

    public int minExtraChar(String s, String[] dictionary) {
        n = s.length();
        // 预处理出左右端点
        lrs = new HashMap<>();
        for (String dict : dictionary) {
            for (int[] tuple : findLR(s, dict)) {
                int l = tuple[0], r = tuple[1] - 1;
                lrs.computeIfAbsent(l, key -> new ArrayList<>()).add(r);
            }
        }

        // 记忆化搜索
        memo = new int[n];
        Arrays.fill(memo, -1);
        return n - dfs(0);
    }

    private int dfs(int i) {
        if (i == n) {
            return 0;
        }
        if (memo[i] != -1) {
            return memo[i];
        }
        // 不选
        int res = dfs(i + 1);
        // 选
        if (lrs.containsKey(i)) {
            for (Integer r : lrs.get(i)) {
                res = Math.max(res, r - i + 1 + dfs(r + 1));
            }
        }
        return memo[i] = res;
    }

    private List<int[]> findLR(String s, String dict) {
        List<int[]> resList = new ArrayList<>();
        int idx = s.indexOf(dict);
        while (idx != -1) {
            resList.add(new int[]{idx, idx + dict.length()});
            idx = s.indexOf(dict, idx + 1);
        }
        return resList;
    }
}

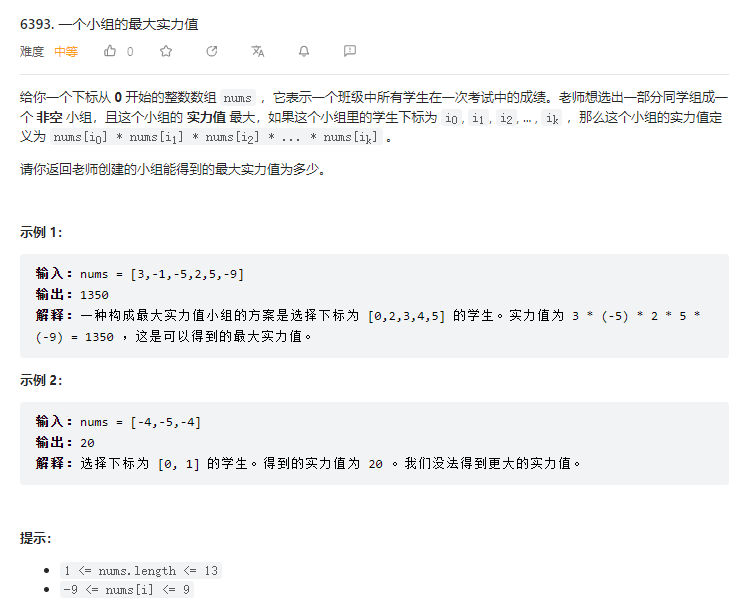
T3. 一个小组的最大实力值（5 分）

解题思路

状态压缩枚举。

时间复杂度：O(2^n)。

也有 O(n) DP 解法 和 O(n) 的贪心解法。

参考代码

class Solution {
    public long maxStrength(int[] nums) {
        int n = nums.length;
        // 不能初始化为 0
        long max = nums[0];
        for (int mask = 1; mask < (1 << n); mask++) {
            long product = 1L;
            for (int k = 0; k < n; k++) {
                if ((mask >> k & 1) == 1) {
                    product *= nums[k];
                }
            }
            max = Math.max(max, product);
        }
        return max;
    }
}

时间复杂度：O(n) 的 DP 解法：

class Solution {
    public long maxStrength(int[] nums) {
        int n = nums.length;
        long max = nums[0], min = nums[0], ans = nums[0];
        for (int i = 1; i < n; i++) {
            long _max = max;
            max = Math.max(max, Math.max(nums[i], Math.max(max * nums[i], min * nums[i])));
            min = Math.min(min, Math.min(nums[i], Math.min(_max * nums[i], min * nums[i])));
        }
        return Math.max(ans, max);
    }
}

T4. 最大公约数遍历（6 分）

解题思路

并查集。相似题目: 1998. 数组的最大公因数排序 https://leetcode.cn/problems/gcd-sort-of-an-array/

时间复杂度：O(nlogA)。

参考代码

class Solution {
    public boolean canTraverseAllPairs(int[] nums) {
        int n = nums.length;

        // 特判
        if (n == 1) return true;
        int min = Arrays.stream(nums).min().orElseThrow();
        if (min == 1) return false;

        int max = Arrays.stream(nums).max().orElseThrow();
        DSU dsu = new DSU(max);
        for (int num : nums) {
            for (int i = 2; i * i <= num; i++) {
                if (num % i == 0) {
                    dsu.union(num, i);
                    dsu.union(num, num / i);
                }
            }
        }

        int root = dsu.find(nums[0]);
        for (int i = 1; i < n; i++) {
            if (dsu.find(nums[i]) == root) continue;
            return false;
        }
        return true;
    }

    private static class DSU {
        int[] fa;
        int sz;

        public DSU(int n) {
            int N = n + 1;
            fa = new int[N];
            for (int i = 0; i < N; i++) {
                fa[i] = i;
            }
            sz = n;
        }

        int find(int x) {
            if (x != fa[x]) {
                fa[x] = find(fa[x]);
            }
            return fa[x];
        }

        void union(int p, int q) {
            int rootP = find(p);
            int rootQ = find(q);
            if (rootP == rootQ) {
                return;
            }
            // 合并到较小的节点
            if (rootP < rootQ) {
                fa[rootQ] = rootP;
            } else {
                fa[rootP] = rootQ;
            }
            sz--;
        }
    }
}

（全文完）