力扣第 113 场双周赛

比赛时间 2023-09-16。本场周赛国服共 314 人 AK。

T1. 使数组成为递增数组的最少右移次数（3 分）

解题思路

第一遍遍历找到最小值下标，第二遍遍历判断是否是递增数组。

时间复杂度：O(n)。

参考代码

class Solution {
    public int minimumRightShifts(List<Integer> nums) {
        int n = nums.size();
        int min = Integer.MAX_VALUE;
        int minI = 0;
        for (int i = 0; i < n; i++) {
            if (min > nums.get(i)) {
                min = nums.get(i);
                minI = i;
            }
        }
        for (int i = 1; i < n; i++) {
            if (nums.get((minI + i - 1) % n) > nums.get((minI + i) % n)) {
                return -1;
            }
        }

        return (n - minI) % n;
    }
}

T2. 删除数对后的最小数组长度（4 分）

解题思路

比赛时狂 WA 6 发。。

将 nums 看作两个数组 a, b，每个 a 连一条线到 b（最小大于 ai 的下标），这些线一定不会交叉。线的数量就是最大配对数。

时间复杂度：O(n)。

题解区有转换成出现次数最多数的频次，O(logn) 的解法。

参考代码

class Solution {
    public int minLengthAfterRemovals(List<Integer> nums) {
        int n = nums.size();
        int c = 0;
        int j = 0;
        for (int i = 0; i < n; i++) {
            j = searchInts(nums, j + 1, nums.get(i));
            if (j < n) c++;
        }
        return Math.max(n % 2, n - c * 2);
    }

    private int searchInts(List<Integer> a, int fromIndex, int key) {
        int l = fromIndex, r = a.size();
        while (l < r) {
            int m = l + (r - l) / 2;
            if (a.get(m) > key) r = m;
            else l = m + 1;
        }
        return l;
    }
}

T3. 统计距离为 k 的点对（5 分）

解题思路

枚举 + 哈希表。k 的范围只有 100，按两数之和的思路来枚举即可。

时间复杂度：O(nk)。

参考代码

class Solution {
    public int countPairs(List<List<Integer>> coordinates, int k) {
        int ans = 0;
        Map<Long, Integer> map = new HashMap<>();
        for (List<Integer> p : coordinates) {
            int x1 = p.get(0), y1 = p.get(1);
            for (int xor_x = 0; xor_x <= k; xor_x++) {
                int xor_y = k - xor_x;
                int x2 = xor_x ^ x1;
                int y2 = xor_y ^ y1;
                long key2 = (long) x2 << 32 | y2;
                ans += map.getOrDefault(key2, 0);
            }
            long key1 = (long) x1 << 32 | y1;
            map.put(key1, map.getOrDefault(key1, 0) + 1);
        }
        return ans;
    }
}

T4. 可以到达每一个节点的最少边反转次数（6 分）

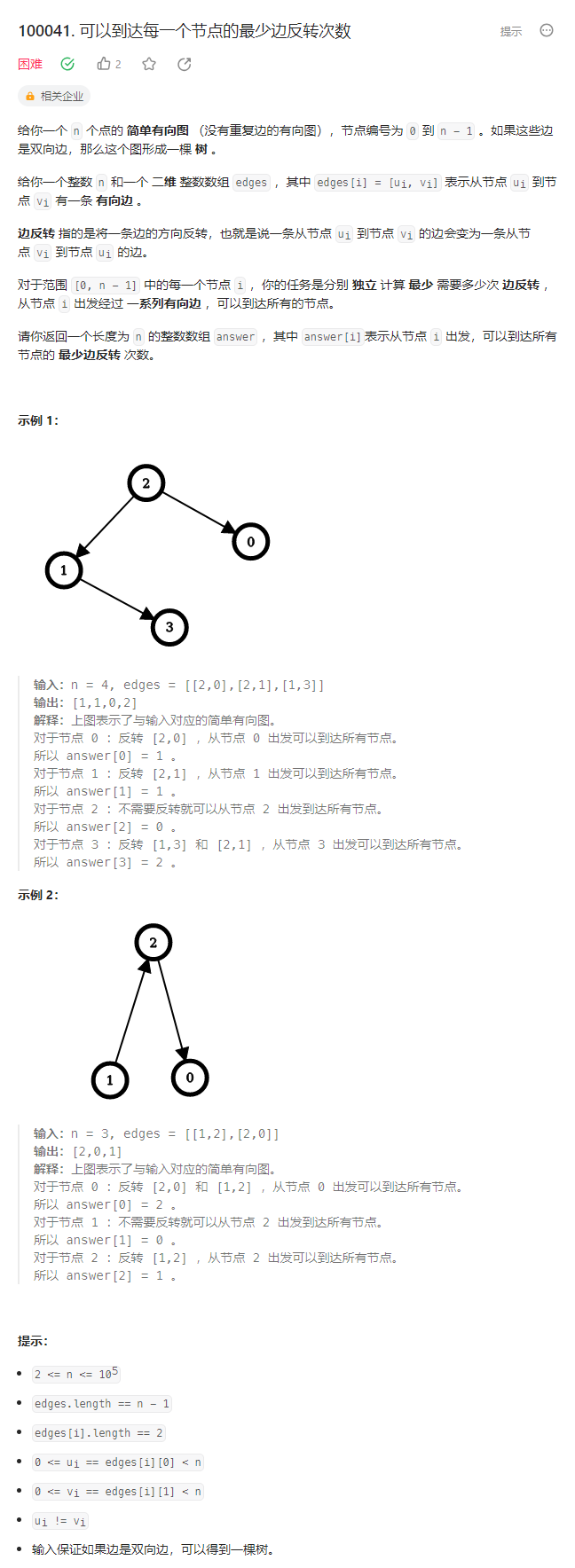
解题思路

换根 DP。

时间复杂度：O(n)。

参考代码

class Solution {
    private List<int[]>[] g;
    private int tot;
    private int[] ans;

    public int[] minEdgeReversals(int n, int[][] edges) {
        g = new List[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int[] e : edges) {
            // 正向权重为 0，反向为 1
            g[e[0]].add(new int[]{e[1], 0});
            g[e[1]].add(new int[]{e[0], 1});
        }

        tot = 0;
        dfs(0, -1);

        ans = new int[n];
        reroot(0, -1, tot);
        return ans;
    }

    private void dfs(int x, int fa) {
        for (int[] p : g[x]) {
            int y = p[0], wt = p[1];
            if (y == fa) continue;
            tot += wt;
            dfs(y, x);
        }
    }

    private void reroot(int x, int fa, int cnt) {
        ans[x] = cnt;
        for (int[] p : g[x]) {
            int y = p[0], wt = p[1];
            if (y == fa) continue;
            reroot(y, x, cnt + (wt == 1 ? -1 : 1));
        }
    }
}

（全文完）