力扣第 123 场双周赛

比赛时间 2024-02-03。本场周赛国服共 503 人 AK。

T1. 三角形类型 II（3 分）

解题思路

分类讨论。

时间复杂度：O(1)。

参考代码

class Solution {
    public String triangleType(int[] nums) {
        Arrays.sort(nums);
        if (nums[0] + nums[1] <= nums[2]) return "none";
        if (nums[0] == nums[1] && nums[0] == nums[2]) return "equilateral";
        if (nums[0] == nums[1] || nums[0] == nums[2] || nums[1] == nums[2]) return "isosceles";
        return "scalene";
    }
}

T2. 人员站位的方案数 I（4 分）

解题思路

二维前缀和。

时间复杂度：O(n^2)。

参考代码

class Solution {
    private int[][] ps2d;

    public int numberOfPairs(int[][] points) {
        int n = 50 + 5;
        int m = 50 + 5;
        int[][] a = new int[n][m];
        for (int[] p : points) {
            a[p[0]][p[1]]++;
        }

        ps2d = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                ps2d[i][j] = ps2d[i - 1][j] + ps2d[i][j - 1] - ps2d[i - 1][j - 1] + a[i - 1][j - 1];
            }
        }

        int ans = 0;
        for (int i = 0; i < points.length; i++) {
            for (int j = 0; j < points.length; j++) {
                if (i == j) continue;
                int x1 = points[i][0], y1 = points[i][1];
                int x2 = points[j][0], y2 = points[j][1];
                if (x1 <= x2 && y2 <= y1) {
                    int sum = sumRegion(x1, y2, x2, y1);
                    if (sum == 2) {
                        ans++;
                    }
                }
            }
        }
        return ans;
    }

    private int sumRegion(int x1, int y1, int x2, int y2) {
        return ps2d[x2 + 1][y2 + 1] - ps2d[x2 + 1][y1] - ps2d[x1][y2 + 1] + ps2d[x1][y1];
    }
}

T3. 最大好子数组和（5 分）

解题思路

哈希分组 + 预处理。分组后，每组由后往前处理 最大值。查询的时候对于每个下标即可 O(logn) / O(1) 查询到最大值。

时间复杂度：O(nlogn) / O(n)。

参考代码

class Solution {
    public long maximumSubarraySum(int[] nums, int k) {
        int n = nums.length;
        long[] ps = new long[n + 1];
        for (int i = 0; i < n; i++) {
            ps[i + 1] = ps[i] + nums[i];
        }

        // 元素出现的下标
        Map<Integer, List<Node>> idsMap = new HashMap<>();
        for (int i = 0; i < n; i++) {
            idsMap.computeIfAbsent(nums[i], e -> new ArrayList<>()).add(new Node(i, 0));
        }
        for (List<Node> ids : idsMap.values()) {
            long mx = Long.MIN_VALUE;
            for (int i = ids.size() - 1; i >= 0; i--) {
                int j = ids.get(i).id;
                mx = Math.max(mx, ps[j + 1]);
                ids.get(i).sum = mx;
            }
        }

        long ans = Long.MIN_VALUE;
        for (int i = 0; i < n; i++) {
            int x = nums[i];

            List<Node> ids = idsMap.getOrDefault(x - k, new ArrayList<>());
            int j = lowerBound(ids, i);
            if (j < ids.size()) {
                ans = Math.max(ans, ids.get(j).sum - ps[i]);
            }

            ids = idsMap.getOrDefault(x + k, new ArrayList<>());
            j = lowerBound(ids, i);
            if (j < ids.size()) {
                ans = Math.max(ans, ids.get(j).sum - ps[i]);
            }
        }
        return ans == Long.MIN_VALUE ? 0 : ans;
    }

    private int lowerBound(List<Node> a, int key) {
        int l = 0, r = a.size();
        while (l < r) {
            int m = l + (r - l) / 2;
            if (a.get(m).id >= key) r = m;
            else l = m + 1;
        }
        return l;
    }

    private static class Node {
        int id;
        long sum;

        public Node(int id, long sum) {
            this.id = id;
            this.sum = sum;
        }
    }
}

T4. 人员站位的方案数 II（7 分）

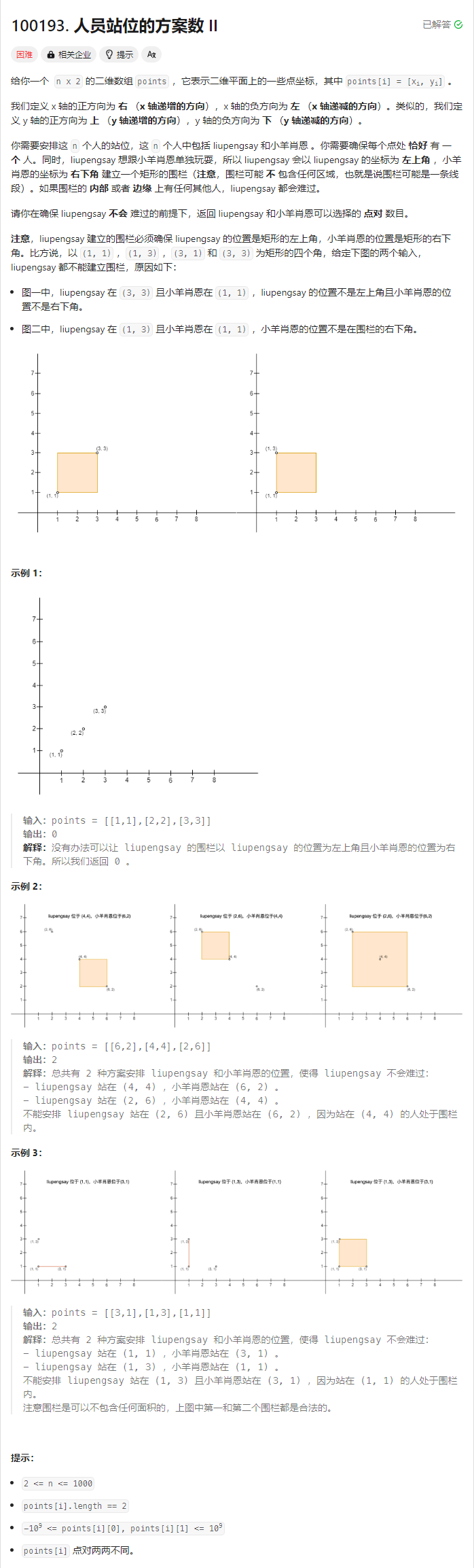
解题思路

离散化 + 二维前缀和。观察到 值域放大到 1e9，但是 n <= 1000，在 T2 上加个离散化处理即可。

时间复杂度：O(n^2)。

参考代码

class Solution {
    private int[][] ps2d;

    public int numberOfPairs(int[][] points) {
        int[] xArr = getDiscrete(points, 0);
        int[] yArr = getDiscrete(points, 1);

        int n = xArr.length + 5;
        int m = yArr.length + 5;
        int[][] a = new int[n][m];
        for (int[] p : points) {
            p[0] = getId(xArr, p[0]);
            p[1] = getId(yArr, p[1]);
            a[p[0]][p[1]]++;
        }

        ps2d = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                ps2d[i][j] = ps2d[i - 1][j] + ps2d[i][j - 1] - ps2d[i - 1][j - 1] + a[i - 1][j - 1];
            }
        }

        int ans = 0;
        for (int i = 0; i < points.length; i++) {
            for (int j = 0; j < points.length; j++) {
                if (i == j) continue;
                int x1 = points[i][0], y1 = points[i][1];
                int x2 = points[j][0], y2 = points[j][1];
                if (x1 <= x2 && y2 <= y1) {
                    int sum = sumRegion(x1, y2, x2, y1);
                    if (sum == 2) {
                        ans++;
                    }
                }
            }
        }
        return ans;
    }

    private int sumRegion(int x1, int y1, int x2, int y2) {
        return ps2d[x2 + 1][y2 + 1] - ps2d[x2 + 1][y1] - ps2d[x1][y2 + 1] + ps2d[x1][y1];
    }

    // x:type=0, y:type=1
    private int[] getDiscrete(int[][] points, int type) {
        Set<Integer> set = new HashSet<>();
        for (int[] p : points) set.add(p[type]);
        int sz = set.size();
        int[] arr = new int[sz];
        int id = 0;
        for (Integer x : set) arr[id++] = x;
        Arrays.sort(arr);
        return arr;
    }

    private int getId(int[] arr, int x) {
        return Arrays.binarySearch(arr, x) + 1;
    }
}

（全文完）