力扣第 131 场双周赛

比赛时间 2024-05-25。本场周赛国服共 171 人 AK。

2~5 月份的事情暂告一段落了，开始复健中。。

T1. 求出出现两次数字的 XOR 值（3 分）

解题思路

模拟。

时间复杂度：O(n)。

参考代码

class Solution {
    public int duplicateNumbersXOR(int[] nums) {
        int[] cnt = new int[55];
        for (int v : nums) {
            cnt[v]++;
        }
        int xor = 0;
        for (int i = 1; i <= 50; i++) {
            if (cnt[i] == 2) {
                xor ^= i;
            }
        }
        return xor;
    }
}

T2. 查询数组中元素的出现位置（4 分）

解题思路

预处理下标。

时间复杂度：O(n)。

参考代码

class Solution {
    public int[] occurrencesOfElement(int[] nums, int[] queries, int x) {
        int n = nums.length;
        List<Integer> posList = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (nums[i] == x) {
                posList.add(i);
            }
        }
        int q = queries.length;
        int[] ans = new int[q];
        Arrays.fill(ans, -1);
        for (int i = 0; i < q; i++) {
            int pos = queries[i] - 1;
            if (pos < posList.size()) {
                ans[i] = posList.get(pos);
            }
        }
        return ans;
    }
}

T3. 所有球里面不同颜色的数目（5 分）

解题思路

双哈希表，一个记录 每个球是什么颜色，一个记录颜色数量。

时间复杂度：O(n)。

参考代码

class Solution {
    public int[] queryResults(int limit, int[][] queries) {
        Map<Integer, Integer> ballColorMap = new HashMap<>();
        Map<Integer, Integer> colorCntMap = new HashMap<>();
        int n = queries.length;
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            int x = queries[i][0], y = queries[i][1];
            if (ballColorMap.containsKey(x)) { // 已染色
                Integer old = ballColorMap.get(x);
                if (colorCntMap.merge(old, -1, Integer::sum) == 0) {
                    colorCntMap.remove(old);
                }
            }
            ballColorMap.put(x, y);
            colorCntMap.merge(y, 1, Integer::sum);
            ans[i] = colorCntMap.size();
        }
        return ans;
    }
}

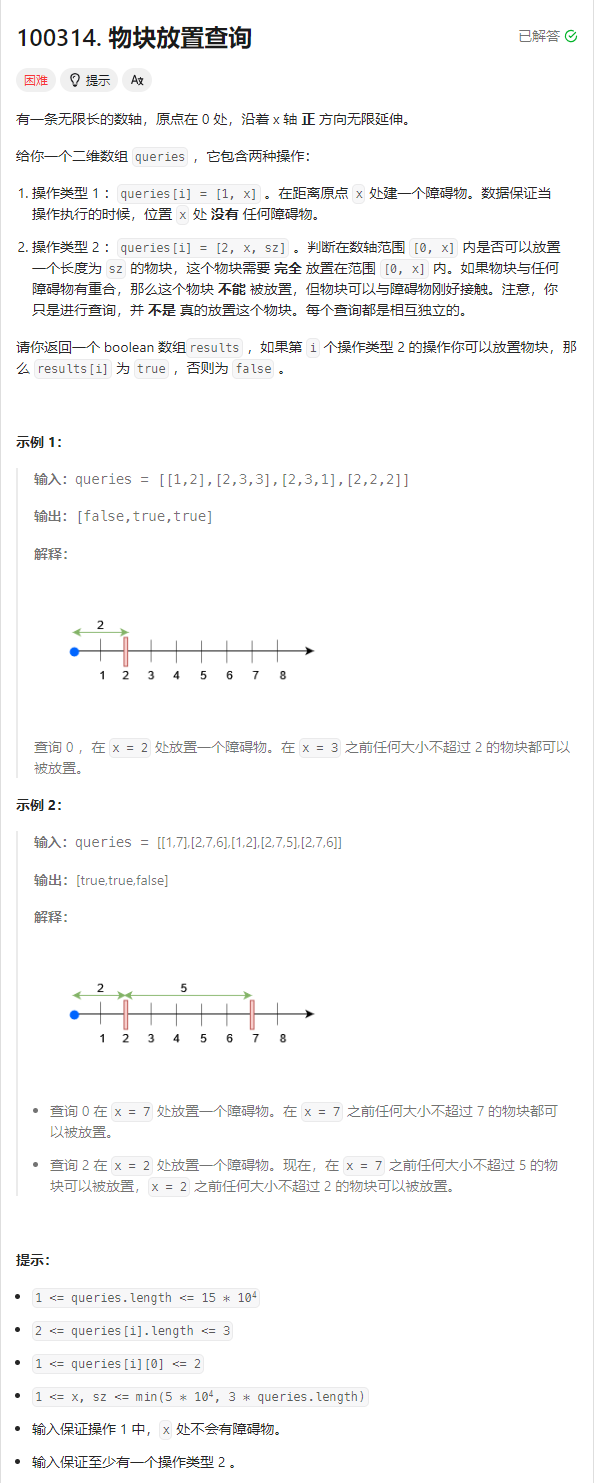
T4. 物块放置查询（8 分）

解题思路

平衡树 + 线段树。

平衡树用于找到插入点的前驱和后继，线段树维护 [0, x] 段最大值。

设插入一个点 x，前驱是 lo，后继是 hi，则长度 L(=hi-lo) 被截断成 L1(=x-lo) + L2(=hi-x)。

时间复杂度：O(qlogq)。

参考代码

class Solution {
    public List<Boolean> getResults(int[][] queries) {
        final int mx = (int) 5e4 + 5;
        final int offset = 1;
        TreeSet<Integer> treeSet = new TreeSet<>();
        treeSet.add(offset); // 哨兵
        treeSet.add(mx); // 哨兵

        SegTree seg = new SegTree(mx);
        List<Boolean> ans = new ArrayList<>(queries.length);
        for (int[] p : queries) {
            int op = p[0], x = p[1] + offset;
            if (op == 1) {
                Integer lower = treeSet.lower(x);
                Integer higher = treeSet.higher(x);
                int L1 = x - lower;
                int L2 = higher - x;
                seg.update(x, x, L1);
                seg.update(higher, higher, L2);
                treeSet.add(x);
            } else {
                int sz = p[2];
                Integer floor = treeSet.floor(x);
                long max_sz = Math.max(seg.getMax(offset, x), x - floor);
                ans.add(max_sz >= sz);
            }
        }
        return ans;
    }

    static class SegTree {
        int n;
        long[] tree, lazy;

        public SegTree(int n) {
            this.n = n;
            this.tree = new long[4 * n];
            this.lazy = new long[4 * n];
        }

        void update(int ql, int qr, int val) {
            update(1, 1, n, ql, qr, val);
        }

        void update(int p, int l, int r, int ql, int qr, int val) {
            if (ql <= l && r <= qr) {
                tree[p] = val;
                lazy[p] = val;
                return;
            }
            pushDown(p);
            int mid = l + (r - l) / 2;
            if (ql <= mid) update(p << 1, l, mid, ql, qr, val);
            if (qr > mid) update(p << 1 | 1, mid + 1, r, ql, qr, val);
            pushUp(p);
        }

        long getMax(int ql, int qr) {
            return getMax(1, 1, n, ql, qr);
        }

        long getMax(int p, int l, int r, int ql, int qr) {
            if (ql <= l && r <= qr) {
                return tree[p];
            }
            pushDown(p);
            int mid = l + (r - l) / 2;
            long max = 0;
            if (ql <= mid) max = Math.max(max, getMax(p << 1, l, mid, ql, qr));
            if (qr > mid) max = Math.max(max, getMax(p << 1 | 1, mid + 1, r, ql, qr));
            return max;
        }

        void pushDown(int p) {
            if (lazy[p] != 0) {
                tree[p << 1] = lazy[p];
                tree[p << 1 | 1] = lazy[p];
                lazy[p << 1] = lazy[p];
                lazy[p << 1 | 1] = lazy[p];
                lazy[p] = 0;
            }
        }

        void pushUp(int p) {
            tree[p] = Math.max(tree[p << 1], tree[p << 1 | 1]);
        }
    }
}

（全文完）