力扣第 147 场双周赛
2025年1月18日大约 4 分钟
力扣第 147 场双周赛
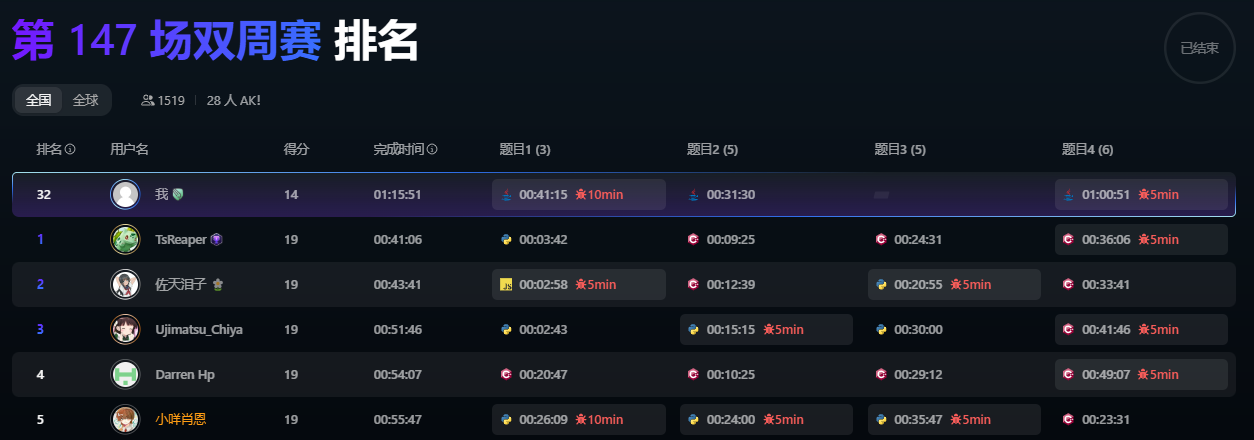
比赛时间 2024-01-04。本场周赛国服共 28 人 AK。
上一次 AK 大概可以追溯到 2024-09-29,第 417 场周赛,240 人 AK,国服 rank 65。随后 AI 选手如苏打般涌现,官方通过加大题目难度来对抗,竟再无 AK 过了。包括本场也没有 AK,但是 PB(Personal best 个人最好成绩),还是记录一下。。

2025 云谷里展新程
T1. 子字符串匹配模式(3 分)

解题思路
库函数 + 分类讨论。
时间复杂度:O(nm)。
参考代码
class Solution {
public boolean hasMatch(String s, String p) {
String[] sp = p.split("\\*");
if (sp.length == 0) return true; // p = "*"
if (sp.length == 1) { // * 在开头或结尾
return s.contains(sp[0]);
}
int i = s.indexOf(sp[0]);
int j = s.lastIndexOf(sp[1]);
if (i < 0 || j < 0) return false;
return i + sp[0].length() <= j;
}
}T2. 设计任务管理器(5 分)

解题思路
哈希表 + 平衡树。
时间复杂度:
- 初始化:
O(nlogn),其中 n 是 tasks 的长度。 - add、edit、rmv 和 execTop:
O(log(n+q)),其中 q 是 add 和 edit 的调用次数之和。
参考代码
class TaskManager {
Map<Integer, Integer> taskId_priority = new HashMap<>();
Map<Integer, Integer> taskId_userId = new HashMap<>();
TreeMap<Integer, TreeSet<Integer>> priority_taskIds = new TreeMap<>(Comparator.reverseOrder());
public TaskManager(List<List<Integer>> tasks) {
for (List<Integer> p : tasks) {
int userId = p.get(0), taskId = p.get(1), priority = p.get(2);
add(userId, taskId, priority);
}
}
public void add(int userId, int taskId, int priority) {
taskId_priority.put(taskId, priority);
taskId_userId.put(taskId, userId);
priority_taskIds.computeIfAbsent(priority, e -> new TreeSet<>(Comparator.reverseOrder())).add(taskId);
}
public void edit(int taskId, int newPriority) {
Integer userId = taskId_userId.get(taskId);
rmv(taskId);
add(userId, taskId, newPriority);
}
public void rmv(int taskId) {
Integer priority = taskId_priority.get(taskId);
taskId_priority.remove(taskId);
taskId_userId.remove(taskId);
priority_taskIds.get(priority).remove(taskId);
if (priority_taskIds.get(priority).isEmpty()) priority_taskIds.remove(priority);
}
public int execTop() {
if (priority_taskIds.isEmpty()) return -1;
Map.Entry<Integer, TreeSet<Integer>> firstEntry = priority_taskIds.firstEntry();
Integer key = firstEntry.getKey();
TreeSet<Integer> priorities = firstEntry.getValue();
Integer taskId = priorities.removeFirst();
if (priorities.isEmpty()) priority_taskIds.remove(key);
return taskId_userId.get(taskId);
}
}
/**
* Your TaskManager object will be instantiated and called as such:
* TaskManager obj = new TaskManager(tasks);
* obj.add(userId,taskId,priority);
* obj.edit(taskId,newPriority);
* obj.rmv(taskId);
* int param_4 = obj.execTop();
*/T3. 最长相邻绝对差递减子序列(5 分)

解题思路
朴素的记忆化搜索是 O(nD^2)。需要优化成 O(nD)。
参考代码
class Solution {
public int longestSubsequence(int[] nums) {
int n = nums.length;
int mx = Arrays.stream(nums).max().orElseThrow();
int maxD = mx - Arrays.stream(nums).min().orElseThrow();
// f[i][j] 表示以 nums[i] 结尾的、最后两个数之差至少为 j 的子序列的最长长度
int[][] f = new int[n][maxD + 2];
// last[x] 表示 x 上一次出现的下标
int[] last = new int[mx + 1];
Arrays.fill(last, -1);
int ans = 0;
for (int i = 0; i < n; i++) {
int x = nums[i];
for (int j = maxD; j >= 0; j--) {
f[i][j] = Math.max(f[i][j + 1], 1);
if (x - j >= 0 && last[x - j] >= 0) {
f[i][j] = Math.max(f[i][j], f[last[x - j]][j] + 1);
}
if (x + j <= mx && last[x + j] >= 0) {
f[i][j] = Math.max(f[i][j], f[last[x + j]][j] + 1);
}
ans = Math.max(ans, f[i][j]);
}
last[x] = i;
}
return ans;
}
}T4. 删除所有值为某个元素后的最大子数组和(6 分)

解题思路
最大子数组和线段树,CF1692H 的板子。
参考代码
class Solution {
public long maxSubarraySum(int[] nums) {
int n = nums.length;
Map<Integer, List<Integer>> posMap = new HashMap<>();
int negCnt = 0;
for (int i = 0; i < n; i++) {
if (nums[i] < 0) {
posMap.computeIfAbsent(nums[i], e -> new ArrayList<>()).add(i);
negCnt++;
}
}
MaxSubArraySegTree seg = new MaxSubArraySegTree(nums);
long ans = seg.query(1, n);
if (negCnt == n) {
return ans;
}
for (Map.Entry<Integer, List<Integer>> entry : posMap.entrySet()) {
Integer val = entry.getKey();
List<Integer> pos = entry.getValue();
for (Integer idx : pos) seg.modify(idx + 1, 0); // 操作
ans = Math.max(ans, seg.query(1, n));
for (Integer idx : pos) seg.modify(idx + 1, val); // 回退
}
return ans;
}
static class MaxSubArraySegTree {
Node[] tree;
static final long INF = (long) 1e18;
static class Node {
// 分别表示 [l,r] 区间:前缀最大子段和,后缀最大子段和,最大子段和,区间和
long maxL, maxR, maxSum, sum;
public Node(long maxL, long maxR, long maxSum, long sum) {
this.maxL = maxL;
this.maxR = maxR;
this.maxSum = maxSum;
this.sum = sum;
}
}
int[] nums;
int n;
public MaxSubArraySegTree(int[] nums) {
this.nums = nums;
this.n = nums.length;
tree = new Node[4 * n];
Arrays.setAll(tree, e -> new Node(-INF, -INF, -INF, -INF));
build(1, 1, n);
}
void build(int p, int l, int r) {
if (l == r) {
int val = nums[l - 1];
tree[p].maxL = tree[p].maxR = tree[p].maxSum = tree[p].sum = val;
return;
}
int mid = l + (r - l) / 2;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
tree[p] = pushUp(tree[p << 1], tree[p << 1 | 1]);
}
// nums[pos] 修改为 val
void modify(int pos, int val) {
modify(1, 1, n, pos, val);
}
void modify(int p, int l, int r, int pos, int val) {
if (l > pos || r < pos) {
return;
}
if (l == pos && r == pos) {
tree[p].maxL = tree[p].maxR = tree[p].maxSum = tree[p].sum = val;
return;
}
int mid = l + (r - l) / 2;
modify(p << 1, l, mid, pos, val);
modify(p << 1 | 1, mid + 1, r, pos, val);
tree[p] = pushUp(tree[p * 2], tree[p * 2 + 1]);
}
// 查询 [l,r] 区间最大子段和
long query(int ql, int qr) {
return query(1, 1, n, ql, qr).maxSum;
}
Node query(int p, int l, int r, int ql, int qr) {
if (l > qr || r < ql) {
return new Node(-INF, -INF, -INF, -INF);
}
if (ql <= l && r <= qr) {
return tree[p];
}
int mid = l + (r - l) / 2;
Node ls = query(p << 1, l, mid, ql, qr);
Node rs = query(p << 1 | 1, mid + 1, r, ql, qr);
return pushUp(ls, rs);
}
Node pushUp(Node ls, Node rs) {
long maxL = Math.max(ls.maxL, ls.sum + rs.maxL);
long maxR = Math.max(rs.maxR, rs.sum + ls.maxR);
// max(l.maxSum, r.maxSum, l.maxR + r.maxL)
long maxSum = Math.max(Math.max(ls.maxSum, rs.maxSum), ls.maxR + rs.maxL);
long sum = ls.sum + rs.sum;
return new Node(maxL, maxR, maxSum, sum);
}
}
}(全文完)