力扣第 84 场双周赛

比赛时间 2022-08-06。本场周赛国服共 770 人 AK。

T1. 合并相似的物品（3 分）

解题思路

TreeMap 一次完成 合并 + 排序。

时间复杂度：O(mnlog(mn))。

参考代码

class Solution {
    public List<List<Integer>> mergeSimilarItems(int[][] items1, int[][] items2) {
        TreeMap<Integer, Integer> treeMap = new TreeMap<>();
        for (int[] ints : items1) {
            treeMap.put(ints[0], treeMap.getOrDefault(ints[0], 0) + ints[1]);
        }
        for (int[] ints : items2) {
            treeMap.put(ints[0], treeMap.getOrDefault(ints[0], 0) + ints[1]);
        }

        List<List<Integer>> resList = new ArrayList<>();
        for (Map.Entry<Integer, Integer> entry : treeMap.entrySet()) {
            resList.add(List.of(entry.getKey(), entry.getValue()));
        }
        return resList;
    }
}

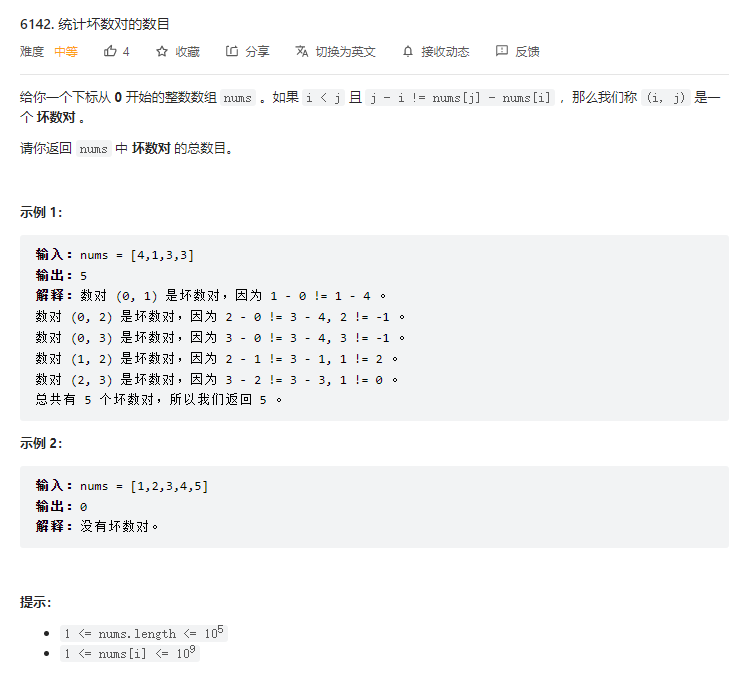
T2. 统计坏数对的数目（5 分）

解题思路

数学。直接求 坏数对 的总数目 并不容易，问题可转化为：坏数对的总数目 = 数对总数目 - 非坏数对的总数目。

非坏数对定义：j - i != nums[j] - nums[i]， 移项得 j - nums[j] == i - nums[i]。

时间复杂度：O(n)。

参考代码

class Solution {
    public long countBadPairs(int[] nums) {
        int len = nums.length;
        Map<Integer, Integer> cntMap = new HashMap<>();
        for (int i = 0; i < len; i++) {
            int diff = i - nums[i];
            cntMap.put(diff, cntMap.getOrDefault(diff, 0) + 1);
        }

        // 总对数
        long total = len * (len - 1L) / 2L;
        // 相同对数
        long same = 0L;
        for (Map.Entry<Integer, Integer> entry : cntMap.entrySet()) {
            int cnt = entry.getValue();
            same += cnt * (cnt - 1L) / 2L;
        }
        return total - same;
    }
}

T3. 任务调度器 II（6 分）

解题思路

贪心。task 能做就做，除非被迫休息。

时间复杂度：O(n)。

参考代码

class Solution {
    public long taskSchedulerII(int[] tasks, int space) {
        // 任务完成时间
        Map<Integer, Long> preMap = new HashMap<>();
        long ans = 0L;
        for (int task : tasks) {
            ans++;
            if (!preMap.containsKey(task)) {
                preMap.put(task, ans);
            } else {
                long pre = preMap.get(task);
                if (ans - pre <= space) {
                    ans = space + pre + 1;
                    preMap.put(task, ans);
                } else {
                    preMap.put(task, ans);
                }
            }
        }
        return ans;
    }
}

T4. 将数组排序的最少替换次数（6 分）

解题思路

贪心。后面的数越大，留给前面的数的空间才越多。因此最后一个数必定不会拆。其他数如果要拆分的话，拆分成 k 个最接近的数。

时间复杂度：O(n)。

参考代码

class Solution {
    public long minimumReplacement(int[] nums) {
        int len = nums.length;
        long ans = 0L;
        int max = nums[len - 1];
        for (int i = len - 1; i >= 0; i--) {
            if (nums[i] <= max) {
                max = nums[i];
                continue;
            }
            // 拆成 k 个数，需要 k-1 次拆分
            int k = (nums[i] + max - 1) / max;
            ans += k - 1;
            max = nums[i] / k;
        }
        return ans;
    }
}

（全文完）