力扣第 85 场双周赛

比赛时间 2022-08-20。本场周赛国服共 571 人 AK。

T1. 得到 K 个黑块的最少涂色次数（3 分）

解题思路

前缀和 + 贪心。

时间复杂度：O(n)。

参考代码

class Solution {
    public int minimumRecolors(String blocks, int k) {
        int len = blocks.length();

        // 预处理
        int[] nums = new int[len];
        for (int i = 0; i < len; i++) {
            if (blocks.charAt(i) == 'B') {
                nums[i] = 1;
            }
        }
        // 前缀和
        int[] preSum = new int[len + 1];
        for (int i = 0; i < len; i++) {
            preSum[i + 1] = preSum[i] + nums[i];
        }

        // 贪心
        int max = 0;
        for (int i = k - 1; i < len; i++) {
            max = Math.max(max, preSum[i + 1] - preSum[i + 1 - k]);
        }
        return k - max;
    }
}

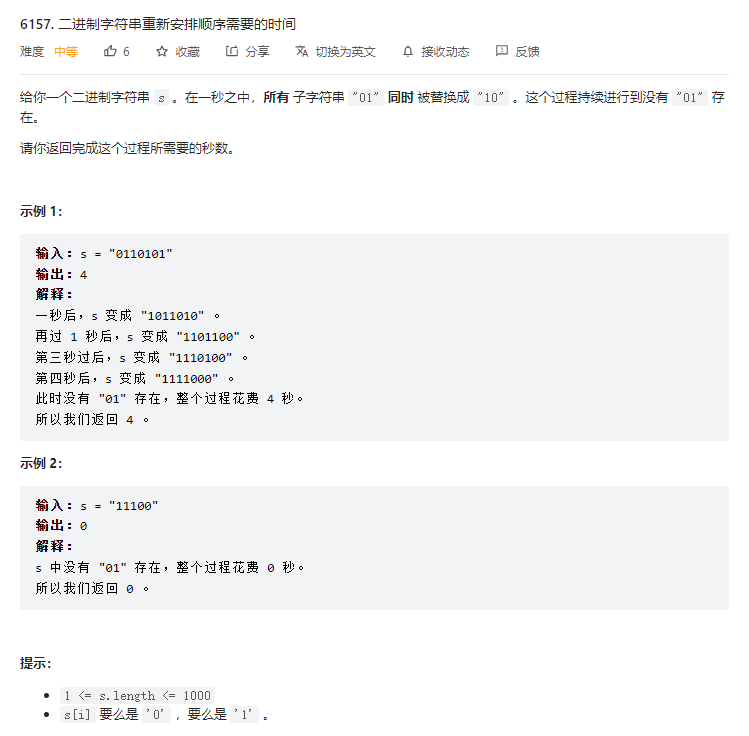
T2. 二进制字符串重新安排顺序需要的时间（4 分）

解题思路

观察到数据范围较小，暴力模拟。

时间复杂度：O(n^2)。

（本题另有线性时间复杂度的解法。

参考代码

class Solution {
    public int secondsToRemoveOccurrences(String s) {
        int cnt = 0;
        while (s.contains("01")) {
            s = s.replace("01", "10");
            cnt++;
        }
        return cnt;
    }
}

T3. 字母移位 II（5 分）

解题思路

差分模拟。在原数组 [i, j] 内加上 inc，等价于在差分数组 diff[i] += inc; diff[j + 1] -= inc;。

时间复杂度：O(n)。

参考代码

class Solution {
    public String shiftingLetters(String s, int[][] shifts) {
        int len = s.length();

        // 差分
        int[] diff = new int[len + 1];
        for (int[] shift : shifts) {
            int i = shift[0];
            int j = shift[1];
            int inc = shift[2] == 0 ? -1 : 1;

            diff[i] += inc;
            diff[j + 1] -= inc;
        }
        // 原数组
        int[] res = new int[len];
        res[0] = diff[0];
        for (int i = 1; i < len; i++) {
            res[i] = res[i - 1] + diff[i];
        }

        char[] chars = s.toCharArray();
        for (int i = 0; i < len; i++) {
            chars[i] = (char) ((((chars[i] - 'a') + res[i]) % 26 + 26) % 26 + 'a');
        }
        return new String(chars);
    }
}

T4. 删除操作后的最大子段和（6 分）

解题思路

比赛时候没想到并查集的做法（在春季赛跌倒的地方（LCP 52. 二叉搜索树染色）又跌倒了一次），套了个最大字段和线段树模板（CF1962H 的简化版）。

时间复杂度：O(nlogn)。

参考代码

class Solution6159 {
    private static final long INF = 100000L * 1000000000L + 10L;

    public long[] maximumSegmentSum(int[] nums, int[] removeQueries) {
        SegmentTree segmentTree = new SegmentTree(nums.length);
        for (int i = 0; i < nums.length; i++) {
            segmentTree.modify(i + 1, nums[i]);
        }

        int len = removeQueries.length;
        long[] res = new long[len];
        for (int i = 0; i < len - 1; i++) {
            segmentTree.modify(removeQueries[i] + 1, -INF);
            res[i] = segmentTree.query().maxSum;
        }
        return res;
    }

    private static class SegmentTree {
        private static class Node {
            // lSum 表示 [l,r] 内以 l 为左端点的最大子段和
            long lSum;
            // rSum 表示 [l,r] 内以 r 为右端点的最大子段和
            long rSum;
            // maxSum 表示 [l,r] 内的最大子段和
            long maxSum;
            // itSum 表示 [l,r] 的区间和
            long itSum;

            public Node(long lSum, long rSum, long maxSum, long itSum) {
                this.lSum = lSum;
                this.rSum = rSum;
                this.maxSum = maxSum;
                this.itSum = itSum;
            }
        }

        private final int N;
        private final Node[] tree;

        public SegmentTree(int n) {
            N = n;
            tree = new Node[4 * N];
            for (int i = 0; i < 4 * N; i++) {
                tree[i] = new Node(0, 0, 0, 0);
            }
            build(1, N, 1);
        }

        private void build(int s, int t, int p) {
            if (s == t) {
                tree[p].lSum = -1;
                tree[p].rSum = -1;
                tree[p].maxSum = -1;
                tree[p].itSum = -1;
                return;
            }
            int mid = s + (t - s) / 2;
            build(s, mid, p * 2);
            build(mid + 1, t, p * 2 + 1);
            tree[p] = pushUp(tree[p * 2], tree[p * 2 + 1]);
        }

        private Node pushUp(Node a, Node b) {
            long lSum = Math.max(a.lSum, a.itSum + b.lSum);
            long rSum = Math.max(b.rSum, b.itSum + a.rSum);
            long maxSum = Math.max(Math.max(a.maxSum, b.maxSum), a.rSum + b.lSum);
            long itSum = a.itSum + b.itSum;
            return new Node(lSum, rSum, maxSum, itSum);
        }

        private void modify(int s, int t, int p, int pos, long val) {
            if (s > pos || t < pos) {
                return;
            }
            if (s == pos && t == pos) {
                tree[p].lSum = val;
                tree[p].rSum = val;
                tree[p].maxSum = val;
                tree[p].itSum = val;
                return;
            }
            int mid = s + (t - s) / 2;
            modify(s, mid, p * 2, pos, val);
            modify(mid + 1, t, p * 2 + 1, pos, val);
            tree[p] = pushUp(tree[p * 2], tree[p * 2 + 1]);
        }

        private Node query(int s, int t, int p, int l, int r) {
            if (s > r || t < l) {
                return new Node(0, 0, 0, 0);
            }
            if (s >= l && t <= r) {
                return tree[p];
            }
            int mid = s + (t - s) / 2;
            Node lSub = query(s, mid, p * 2, l, r);
            Node rSub = query(mid + 1, t, p * 2 + 1, l, r);
            return pushUp(lSub, rSub);
        }

        private void modify(int pos, long val) {
            modify(1, N, 1, pos, val);
        }

        private Node query() {
            return query(1, N, 1, 1, N);
        }
    }
}

（全文完）