力扣第 86 场双周赛

比赛时间 2022-09-03。本场周赛国服共 757 人 AK。

T1. 和相等的子数组（3 分）

解题思路

HashSet 模拟。

时间复杂度：O(n)。

参考代码

class Solution {
    public boolean findSubarrays(int[] nums) {
        int len = nums.length;
        Set<Integer> sumSet = new HashSet<>();
        for (int i = 1; i < len; i++) {
            int sum = nums[i - 1] + nums[i];
            if (sumSet.contains(sum)) {
                return true;
            }
            sumSet.add(sum);
        }
        return false;
    }
}

T2. 严格回文的数字（4 分）

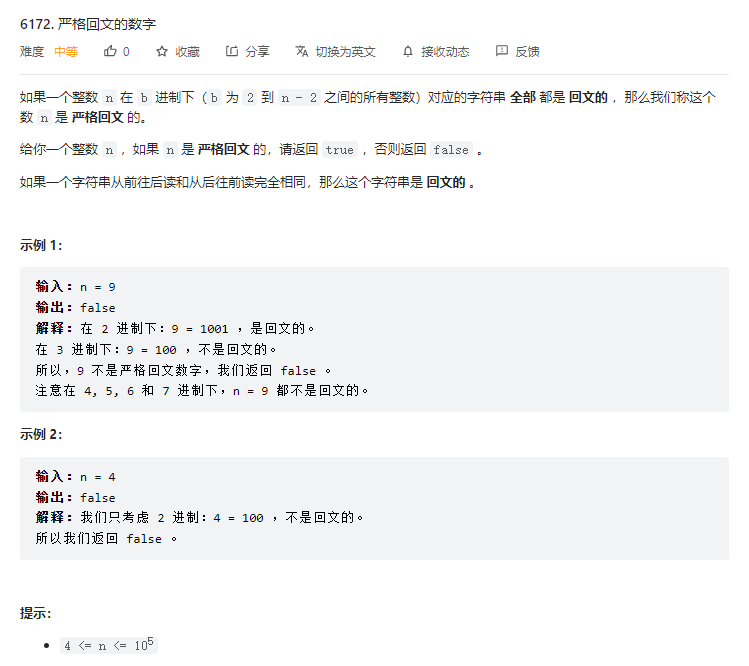
解题思路

脑筋急转弯。

• 当 n > 4 时，n-2 进制均为 12，不是回文的；
• 当 n = 4 时，2 进制为 100，不是回文的；

时间复杂度：O(1)。

参考代码

class Solution {
    public boolean isStrictlyPalindromic(int n) {
        return false;
    }
}

T3. 被列覆盖的最多行数（5 分）

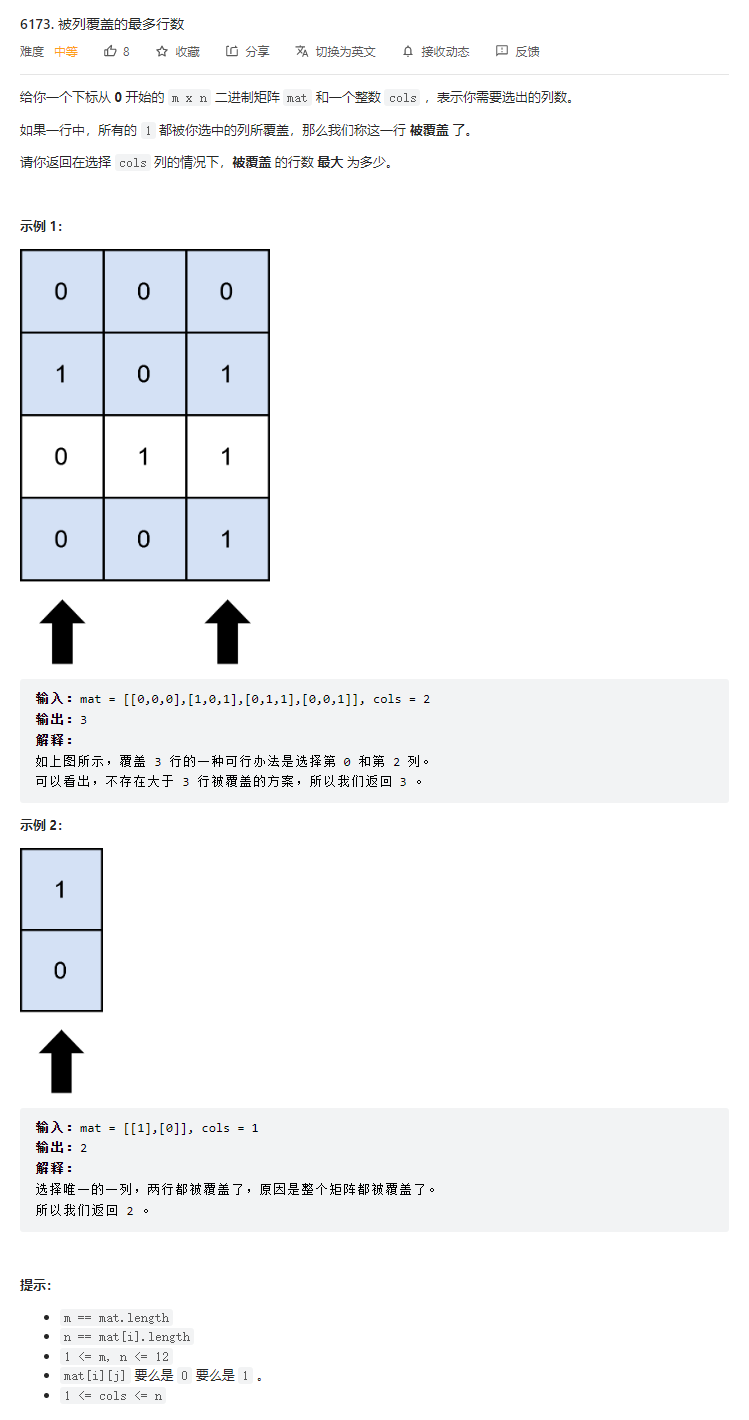
解题思路

状态压缩枚举。

时间复杂度：O(m*2^n)。本题理论上界为 12 * 2^12 = 49152。

参考代码

class Solution {
    public int maximumRows(int[][] mat, int cols) {
        int m = mat.length;
        int n = mat[0].length;

        // 预处理 第 i 行有多少个 1
        int[] cnt1 = new int[m];
        for (int i = 0; i < m; i++) {
            int sum = 0;
            for (int j = 0; j < n; j++) {
                if (mat[i][j] == 1) {
                    sum++;
                }
            }
            cnt1[i] = sum;
        }

        // 选取 cols 列
        int max = 0;
        for (int state = 0; state < (1 << n); state++) {
            if (Integer.bitCount(state) != cols) {
                continue;
            }
            int cnt = 0;
            for (int i = 0; i < m; i++) {
                int sum = 0;
                // 第 k 位被选中
                for (int k = 0; k < n; k++) {
                    if (((state >> k) & 1) == 1) {
                        if (mat[i][k] == 1) {
                            sum++;
                        }
                    }
                }
                if (sum == cnt1[i]) {
                    cnt++;
                }
            }
            max = Math.max(max, cnt);
        }
        return max;
    }
}

灵神直播介绍的黑科技 Gosper's Hack 时间复杂度 O(1) 找到下一个大小为 cols 的集合：

class Solution {
    public int maximumRows(int[][] mat, int cols) {
        int m = mat.length;
        int n = mat[0].length;

        // 预处理 第 i 行有多少个 1
        int[] cnt1 = new int[m];
        for (int i = 0; i < m; i++) {
            int sum = 0;
            for (int j = 0; j < n; j++) {
                if (mat[i][j] == 1) {
                    sum++;
                }
            }
            cnt1[i] = sum;
        }

        // 选取 cols 列
        int max = 0;
        int state = (1 << cols) - 1;

        while (state < (1 << n)) {
            int cnt = 0;
            for (int i = 0; i < m; i++) {
                int sum = 0;
                // 第 k 位被选中
                for (int k = 0; k < n; k++) {
                    if (((state >> k) & 1) == 1) {
                        if (mat[i][k] == 1) {
                            sum++;
                        }
                    }
                }
                if (sum == cnt1[i]) {
                    cnt++;
                }
            }
            max = Math.max(max, cnt);

            // Gosper's Hack 时间复杂度 O(1) 找到下一个大小为 cols 的集合
            int lowbit = state & -state;
            int x = state + lowbit;
            state = (state ^ x) / lowbit >> 2 | x;
        }
        return max;
    }
}

T4. 预算内的最多机器人数目（6 分）

解题思路

二分 + 单调队列。单调队列维护区间最大值。思路来自第 239 题。

时间复杂度：O(nlogn)。

参考代码

class Solution {
    public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
        int n = chargeTimes.length;

        int left = 1;
        int right = n + 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            // 边界二分 F, F,..., F, [T, T,..., T]
            // ----------------------^
            if (!checkMid(chargeTimes, runningCosts, budget, mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left - 1;
    }

    // true: 可以连续运行 k 个机器人
    private boolean checkMid(int[] chargeTimes, int[] runningCosts, long budget, int k) {
        int n = chargeTimes.length;

        // 滑动窗口最大值
        Deque<Integer> deque = new ArrayDeque<>();
        long max = 0;
        long sum = 0;

        // 前 k 个
        for (int i = 0; i < k; i++) {
            while (!deque.isEmpty() && chargeTimes[i] >= chargeTimes[deque.getLast()]) {
                deque.removeLast();
            }
            deque.addLast(i);
            sum += runningCosts[i];
        }

        max = chargeTimes[deque.getFirst()];
        if (max + k * sum <= budget) {
            return true;
        }

        // k+1 到 len
        for (int i = k; i < n; i++) {
            while (!deque.isEmpty() && chargeTimes[i] >= chargeTimes[deque.getLast()]) {
                deque.removeLast();
            }
            deque.addLast(i);
            while (deque.getFirst() <= i - k) {
                deque.removeFirst();
            }

            max = chargeTimes[deque.getFirst()];
            sum = sum + runningCosts[i] - runningCosts[i - k];

            long totalCost = max + k * sum;
            if (totalCost <= budget) {
                return true;
            }
        }
        return false;
    }
}

（全文完）