力扣第 87 场双周赛

比赛时间 2022-09-17。本场周赛国服共 448 人 AK。

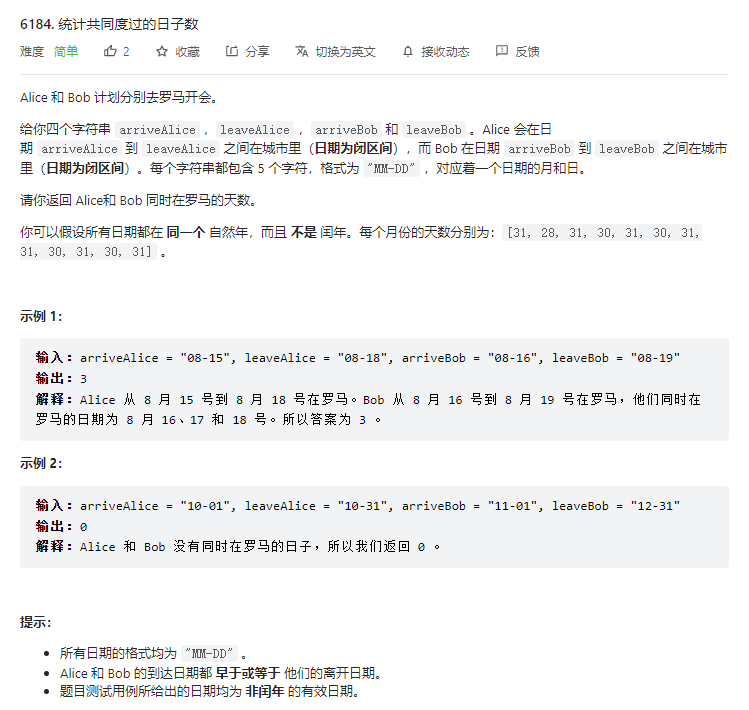
T1. 统计共同度过的日子数（3 分）

解题思路

模拟。把日期转化为一年中的第 n 天（即下标），再求交集即可。

时间复杂度：O(1)。

参考代码

class Solution {
    private static final int MAX_N = 12;
    private static final int[] DAYS = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
    private int[] preSum;

    public int countDaysTogether(String arriveAlice, String leaveAlice, String arriveBob, String leaveBob) {
        // 前缀和
        preSum = new int[MAX_N + 1];
        for (int i = 0; i < MAX_N; i++) {
            preSum[i + 1] = preSum[i] + DAYS[i];
        }

        // 线段取交集
        int arriveMax = Math.max(getIdx(arriveAlice), getIdx(arriveBob));
        int leaveMin = Math.min(getIdx(leaveAlice), getIdx(leaveBob));
        return Math.max(0, leaveMin - arriveMax + 1);
    }

    private int getIdx(String s) {
        int month = Integer.parseInt(s.substring(0, 2));
        int day = Integer.parseInt(s.substring(3, 5));
        return preSum[month - 1] + day;
    }
}

T2. 运动员和训练师的最大匹配数（4 分）

解题思路

排序 + 双指针。

时间复杂度：O(nlogn)。为排序时间复杂度。

参考代码

class Solution {
    public int matchPlayersAndTrainers(int[] players, int[] trainers) {
        Arrays.sort(players);
        Arrays.sort(trainers);

        // 双指针
        int p1 = 0;
        int p2 = 0;
        int cnt = 0;
        while (p1 < players.length && p2 < trainers.length) {
            if (players[p1] <= trainers[p2]) {
                cnt++;
                p1++;
                p2++;
            } else {
                p2++;
            }
        }
        return cnt;
    }
}

T3. 按位或最大的最小子数组长度（5 分）

解题思路

难点在于需要在时间复杂度 O(1) 内知道区间的按位或，比赛时用了前缀和思想 + 二分查找求解。

时间复杂度：O(nlogn)。常数为 logmax(nums) 可看作 30。

参考代码

class Solution {
    private static final int MAX_N = 31;

    public int[] smallestSubarrays(int[] nums) {
        int n = nums.length;

        int[][] bitCnt = new int[n][MAX_N];
        for (int i = 0; i < n; i++) {
            for (int k = 0; k < MAX_N; k++) {
                if (((nums[i] >> k) & 1) == 1) {
                    bitCnt[i][k]++;
                }
            }
        }

        int[][] preSum = new int[n + 1][MAX_N];
        for (int i = 0; i < n; i++) {
            for (int k = 0; k < MAX_N; k++) {
                preSum[i + 1][k] = preSum[i][k] + bitCnt[i][k];
            }
        }

        int[] res = new int[n];
        for (int i = 0; i < n; i++) {
            // [i, n-1] 最大按位或
            int max = 0;
            for (int k = 0; k < MAX_N; k++) {
                if (preSum[n][k] - preSum[i][k] > 0) {
                    max++;
                }
            }

            // 二分
            int left = i;
            int right = n;
            while (left < right) {
                int mid = left + (right - left) / 2;
                // 边界二分 F, F,..., F, [T, T,..., T]
                // ----------------------^
                if (checkMid(preSum, i, max, mid)) {
                    right = mid;
                } else {
                    left = mid + 1;
                }
            }
            res[i] = left - i + 1;
        }
        return res;
    }

    // FFFTTT
    private boolean checkMid(int[][] preSum, int i, int max, int mid) {
        int cnt = 0;
        for (int k = 0; k < MAX_N; k++) {
            if (preSum[mid + 1][k] - preSum[i][k] > 0) {
                cnt++;
            }
        }
        return cnt == max;
    }
}

灵佬直播分享了一种解法，时间复杂度：O(n*logmax(nuns))，空间复杂度：O(logmax(nuns))，消化中：

class Solution {
    public int[] smallestSubarrays(int[] nums) {
        int n = nums.length;

        int[] res = new int[n];
        List<int[]> ors = new ArrayList<>();
        for (int i = n - 1; i >= 0; i--) {
            int num = nums[i];
            ors.add(new int[]{0, i});
            int k = 0;
            for (int[] or : ors) {
                or[0] |= num;
                if (ors.get(k)[0] == or[0]) {
                    ors.get(k)[1] = or[1];
                } else {
                    k++;
                    ors.set(k, or);
                }
            }
            ors.subList(k + 1, ors.size()).clear();
            res[i] = ors.get(0)[1] - i + 1;
        }
        return res;
    }
}

T4. 完成所有交易的初始最少钱数（6 分）

解题思路

贪心。思考：如何才能尽可能亏得多？

对于亏钱的交易，亏钱多的越早越好，对于赚钱的交易，收益越高的越晚越好。先进行完所有亏钱交易，再进行赚钱交易。按顺序贪心取最小值即可。

时间复杂度：O(nlogn)。为排序时间复杂度。

参考代码

class Solution {
    public long minimumMoney(int[][] transactions) {
        List<int[]> negativeList = new ArrayList<>();
        List<int[]> positiveList = new ArrayList<>();
        for (int[] transaction : transactions) {
            if (transaction[1] - transaction[0] <= 0) {
                negativeList.add(transaction);
            } else {
                positiveList.add(transaction);
            }
        }
        negativeList.sort(Comparator.comparingInt(o -> o[1]));
        positiveList.sort((o1, o2) -> Integer.compare(o2[0], o1[0]));

        long money = 0;
        long min = Long.MAX_VALUE;
        for (int[] ints : negativeList) {
            money -= ints[0];
            min = Math.min(min, money);
            money += ints[1];
        }
        for (int[] ints : positiveList) {
            money -= ints[0];
            min = Math.min(min, money);
            money += ints[1];
        }
        return -min;
    }
}

（全文完）