力扣第 88 场双周赛
2023年12月17日大约 4 分钟
力扣第 88 场双周赛

比赛时间 2022-10-01。本场周赛国服共 686 人 AK。
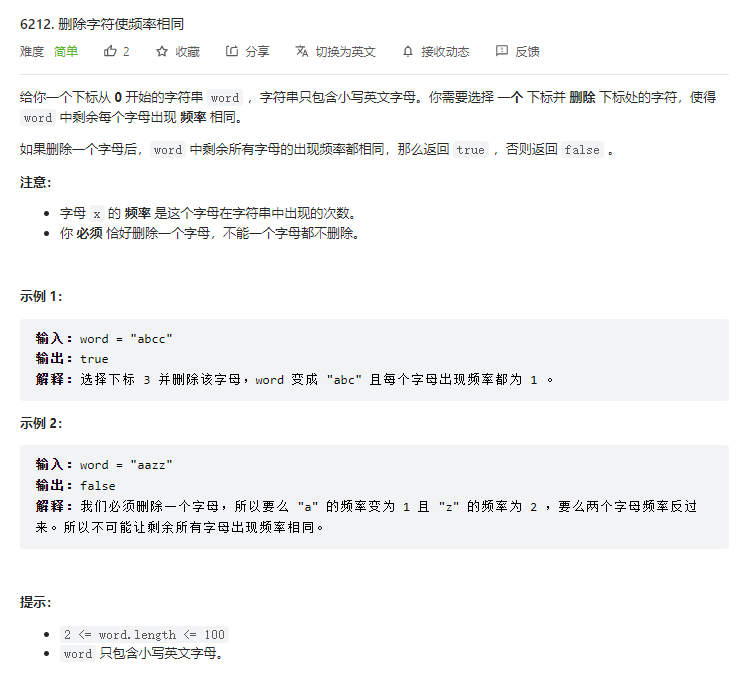
T1. 删除字符使频率相同(3 分)
解题思路
暴力模拟。枚举每个下标被删除后是否满足即可。
时间复杂度:O(n^2)。
参考代码
class Solution {
public boolean equalFrequency(String word) {
int len = word.length();
for (int i = 0; i < len; i++) {
Map<Character, Integer> cntMap = new HashMap<>();
for (int j = 0; j < len; j++) {
if (i == j) {
continue;
}
char ch = word.charAt(j);
cntMap.put(ch, cntMap.getOrDefault(ch, 0) + 1);
}
if (check(cntMap)) {
return true;
}
}
return false;
}
private boolean check(Map<Character, Integer> cntMap) {
int pre = -1;
for (Map.Entry<Character, Integer> entry : cntMap.entrySet()) {
if (pre == -1) {
pre = entry.getValue();
} else {
if (entry.getValue() != pre) {
return false;
}
}
}
return true;
}
}T2. 最长上传前缀(4 分)

解题思路
并查集。联通分量总是合并到更小的节点。最后 1 的联通分量大小即为 最长上传前缀 的长度。
时间复杂度:O(nlogn)。
参考代码
class LUPrefix {
private final int n;
private final DSU dsu;
public LUPrefix(int n) {
this.n = n;
dsu = new DSU(n);
}
public void upload(int video) {
// 每个视频编号为 1 到 n 之间的 不同 数字。映射到 0 ~ n-1
video--;
dsu.sz[video]++;
// dsu.sz[i] > 0 表示 i 已经上传
if (video + 1 < n && dsu.sz[video + 1] > 0) {
dsu.union(video, video + 1);
}
if (video - 1 >= 0 && dsu.sz[video - 1] > 0) {
dsu.union(video, video - 1);
}
}
public int longest() {
return dsu.sz[0];
}
private static class DSU {
// 父节点数组/祖先数组
int[] fa;
int[] sz;
// 初始化
public DSU(int n) {
fa = new int[n];
for (int i = 0; i < n; i++) {
fa[i] = i;
}
sz = new int[n];
}
// 查找
int find(int x) {
// 路径压缩
if (x != fa[x]) {
fa[x] = find(fa[x]);
}
return fa[x];
}
// 合并
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) {
return;
}
// 合并到更小的节点
if (rootP < rootQ) {
fa[rootQ] = rootP;
sz[rootP] += sz[rootQ];
} else {
fa[rootP] = rootQ;
sz[rootQ] += sz[rootP];
}
}
}
}
/**
* Your LUPrefix object will be instantiated and called as such:
* LUPrefix obj = new LUPrefix(n);
* obj.upload(video);
* int param_2 = obj.longest();
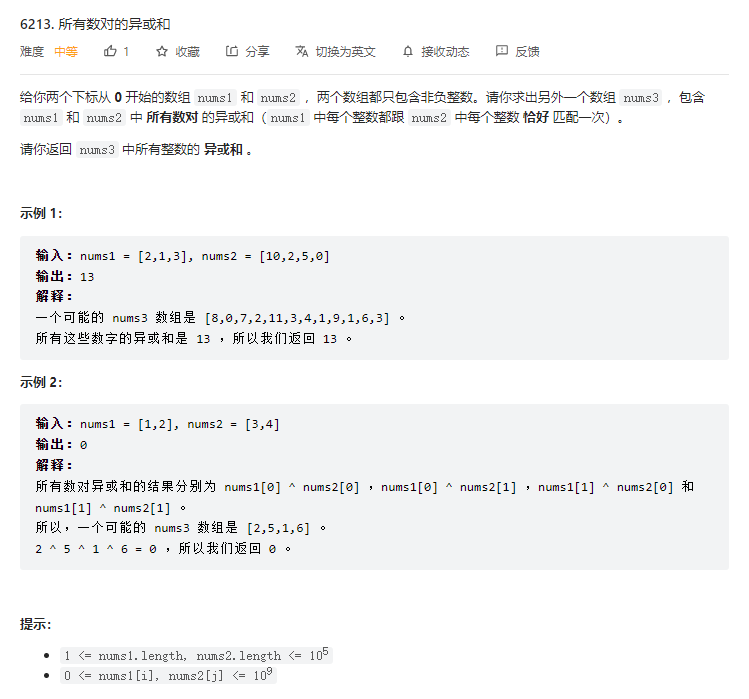
*/T3. 所有数对的异或和(5 分)
解题思路
贪心。如果 nums1 的元素个数为偶数,那么 nums2 每个元素出现次数同样为偶数,根据 a^b^b=a 性质得,同一个数偶数次异或并不影响结果。因此只考虑奇数次情况即可。
时间复杂度:O(n + m)。最坏情况时,结果为所有数的异或和。
参考代码
class Solution {
public int xorAllNums(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
if (len1 % 2 == 1 && len2 % 2 == 1) {
return xorAllNums(nums2) ^ xorAllNums(nums1);
} else if (len1 % 2 == 1) {
return xorAllNums(nums2);
} else if (len2 % 2 == 1) {
return xorAllNums(nums1);
} else {
return 0;
}
}
private int xorAllNums(int[] nums) {
int res = nums[0];
for (int i = 1; i < nums.length; i++) {
res ^= nums[i];
}
return res;
}
}T4. 满足不等式的数对数目(6 分)

解题思路
根据 nums1[i] - nums1[j] <= nums2[i] - nums2[j] + diff,移项得 (nums1[i] - nums2[i]) <= (nums1[j] - nums2[j]) + diff,预处理每个 (nums1[i] - nums2[i]) 为 a[i] 结果为 a[i] <= a[j] + diff。即经典逆序对问题,可通过归并/树状数组/线段树求解。本题使用动态开点线段树 + 偏移量求解。
时间复杂度:O(nlogn)。
参考代码
class Solution {
private static final int OFFSET = (int) 1e4 * 3 + 5;
public long numberOfPairs(int[] nums1, int[] nums2, int diff) {
int n = nums1.length;
int[] nums1sub2 = new int[n];
for (int i = 0; i < n; i++) {
nums1sub2[i] = nums1[i] - nums2[i];
}
DynamicSegTreeAdd dynamicSegTreeAdd = new DynamicSegTreeAdd();
long res = 0;
for (int i = 0; i < n; i++) {
int idx = nums1sub2[i] + OFFSET;
res += dynamicSegTreeAdd.getSum(1, idx);
dynamicSegTreeAdd.add(idx - diff, idx - diff, 1);
}
return res;
}
private static class DynamicSegTreeAdd {
private static final int N = Integer.MAX_VALUE;
private final Node root = new Node();
private static class Node {
Node ls, rs;
long sum, max, lazy;
}
// 区间 [l,r] 置为 val
public void add(int l, int r, int val) {
this.add(l, r, val, 1, N, root);
}
// 区间 [l,r] 求和
public long getSum(int l, int r) {
return this.getSum(l, r, 1, N, root);
}
// 区间 [l,r] 最大值
public long getMax(int l, int r) {
return this.getMax(l, r, 1, N, root);
}
private void add(int l, int r, int val, int s, int t, Node node) {
if (l <= s && t <= r) {
node.sum += (t - s + 1L) * val;
node.max += val;
node.lazy += val;
return;
}
int mid = s + (t - s) / 2;
pushDown(node, s, t, mid);
if (l <= mid) {
add(l, r, val, s, mid, node.ls);
}
if (r > mid) {
add(l, r, val, mid + 1, t, node.rs);
}
pushUp(node);
}
private long getSum(int l, int r, int s, int t, Node node) {
if (l <= s && t <= r) {
return node.sum;
}
int mid = s + (t - s) / 2;
pushDown(node, s, t, mid);
long sum = 0;
if (l <= mid) {
sum = getSum(l, r, s, mid, node.ls);
}
if (r > mid) {
sum += getSum(l, r, mid + 1, t, node.rs);
}
return sum;
}
private long getMax(int l, int r, int s, int t, Node node) {
if (l <= s && t <= r) {
return node.max;
}
int mid = s + (t - s) / 2;
pushDown(node, s, t, mid);
long max = 0;
if (l <= mid) {
max = getMax(l, r, s, mid, node.ls);
}
if (r > mid) {
max = Math.max(max, getMax(l, r, mid + 1, t, node.rs));
}
return max;
}
private void pushDown(Node node, int s, int t, int mid) {
if (node.ls == null) {
node.ls = new Node();
}
if (node.rs == null) {
node.rs = new Node();
}
if (node.lazy > 0) {
node.ls.sum += node.lazy * (mid - s + 1L);
node.rs.sum += node.lazy * (t - mid);
node.ls.max += node.lazy;
node.rs.max += node.lazy;
node.ls.lazy += node.lazy;
node.rs.lazy += node.lazy;
node.lazy = 0;
}
}
private void pushUp(Node node) {
node.sum = node.ls.sum + node.rs.sum;
node.max = Math.max(node.ls.max, node.rs.max);
}
}
}(全文完)