力扣第 308 场周赛

比赛时间 2022-08-28。本场周赛国服共 1311 人 AK。

T1. 和有限的最长子序列（3 分）

解题思路

排序 + 前缀和 + 二分。根据贪心思想，子序列 的 最大 长度必然由最小的数组成。

时间复杂度：O(nlogn)。

参考代码

class Solution {
    public int[] answerQueries(int[] nums, int[] queries) {
        int n = nums.length;
        int m = queries.length;

        Arrays.sort(nums);

        int[] preSum = new int[n + 1];
        for (int i = 0; i < n; i++) {
            preSum[i + 1] = preSum[i] + nums[i];
        }

        int[] answer = new int[m];
        for (int i = 0; i < m; i++) {
            answer[i] = binarySearch(preSum, queries[i]);
        }
        return answer;
    }

    private int binarySearch(int[] preSum, int query) {
        int left = 0;
        int right = preSum.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            // 边界二分 F, F,..., F, [T, T,..., T]
            // ----------------------^
            if (preSum[mid] > query) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left - 1;
    }
}

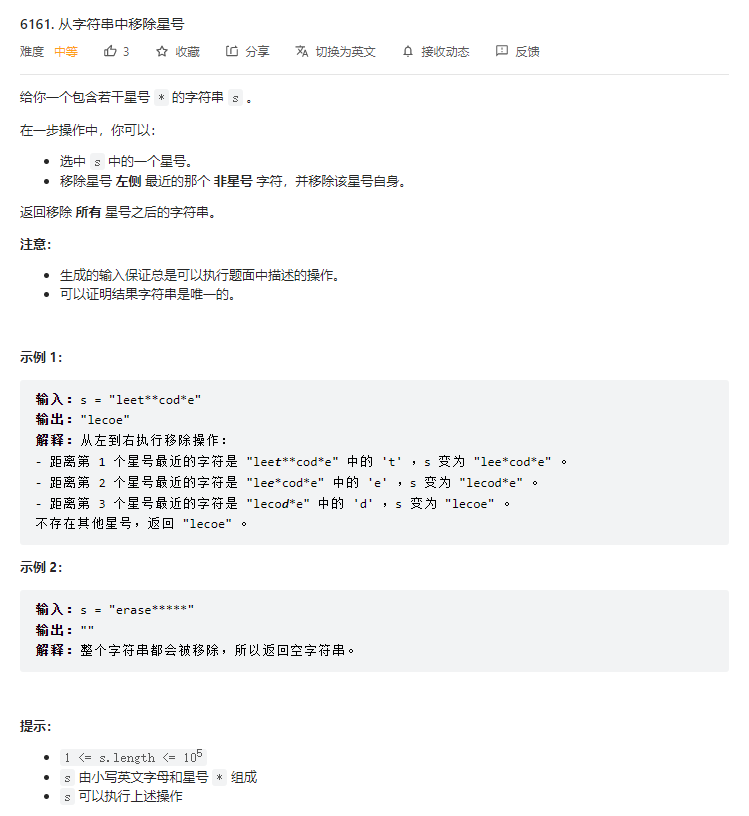
T2. 从字符串中移除星号（4 分）

解题思路

栈思想，后往前枚举，遇到一个星号代表可以忽略一个非星号字符。

时间复杂度：O(n)。

参考代码

class Solution {
    public String removeStars(String s) {
        int len = s.length();
        int del = 0;
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = len - 1; i >= 0; i--) {
            char ch = s.charAt(i);
            if (ch == '*') {
                del++;
            } else if (del > 0) {
                del--;
            } else {
                stringBuilder.append(ch);
            }
        }
        return stringBuilder.reverse().toString();
    }
}

T3. 收集垃圾的最少总时间（4 分）

解题思路

贪心+前缀和。因为每辆垃圾车都从房子 0 出发，因此找出每辆垃圾车最后需要到达的房子即可。

时间复杂度：O(n)。

参考代码

class Solution {
    public int garbageCollection(String[] garbage, int[] travel) {
        int len = garbage.length;

        int mCnt = 0;
        int pCnt = 0;
        int gCnt = 0;
        List<Integer> mList = new ArrayList<>();
        List<Integer> pList = new ArrayList<>();
        List<Integer> gList = new ArrayList<>();
        for (int i = 0; i < len; i++) {
            boolean isM = false;
            boolean isP = false;
            boolean isG = false;
            for (char ch : garbage[i].toCharArray()) {
                if (ch == 'M') {
                    mCnt++;
                    isM = true;
                } else if (ch == 'P') {
                    pCnt++;
                    isP = true;
                } else if (ch == 'G') {
                    gCnt++;
                    isG = true;
                }
            }
            if (isM) {
                mList.add(i);
            }
            if (isP) {
                pList.add(i);
            }
            if (isG) {
                gList.add(i);
            }
        }

        int[] preSum = new int[len];
        for (int i = 0; i < len - 1; i++) {
            preSum[i + 1] = preSum[i] + travel[i];
        }

        int res = 0;
        if (mCnt > 0) {
            int lastM = mList.get(mList.size() - 1);
            res += preSum[lastM] + mCnt;
        }
        if (pCnt > 0) {
            int lastP = pList.get(pList.size() - 1);
            res += preSum[lastP] + pCnt;
        }
        if (gCnt > 0) {
            int lastG = gList.get(gList.size() - 1);
            res += preSum[lastG] + gCnt;
        }
        return res;
    }
}

T4. 给定条件下构造矩阵（6 分）

解题思路

对行和列分别拓扑排序，再构造 k*k 矩阵即可。

时间复杂度：O(k^2)。上界为最后构造答案的时间复杂度。

参考代码

class Solution {
    public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {
        // 拓扑排序
        int[] rowTopo = topo(k, rowConditions);
        if (rowTopo.length == 0) {
            return new int[0][];
        }
        int[] colTopo = topo(k, colConditions);
        if (colTopo.length == 0) {
            return new int[0][];
        }

        // 预处理坐标
        int[] rowIdx = new int[k + 1];
        for (int i = 0; i < k; i++) {
            rowIdx[rowTopo[i]] = i;
        }
        int[] colIdx = new int[k + 1];
        for (int i = 0; i < k; i++) {
            colIdx[colTopo[i]] = i;
        }

        // 生成答案
        int[][] ans = new int[k][k];
        for (int num = 1; num <= k; num++) {
            ans[rowIdx[num]][colIdx[num]] = num;
        }
        return ans;
    }

    private int[] topo(int k, int[][] conditions) {
        // 拓扑排序
        Map<Integer, List<Integer>> outGraph = new HashMap<>();
        // 两个数组里的整数都是 1 到 k 之间的数字。
        int[] inDegrees = new int[k + 1];

        // 其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。
        for (int[] prerequisite : conditions) {
            int from = prerequisite[0];
            int to = prerequisite[1];
            outGraph.computeIfAbsent(from, key -> new ArrayList<>()).add(to);
            inDegrees[to]++;
        }

        // 入度为 0 进队列。记为 0 到 numCourses - 1
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 1; i <= k; i++) {
            if (inDegrees[i] == 0) {
                queue.add(i);
            }
        }
        List<Integer> resList = new ArrayList<>();
        while (!queue.isEmpty()) {
            int cur = queue.remove();
            resList.add(cur);

            for (int next : outGraph.getOrDefault(cur, new ArrayList<>())) {
                inDegrees[next]--;
                if (inDegrees[next] == 0) {
                    queue.add(next);
                }
            }
        }
        if (resList.size() == k) {
            return resList.stream().mapToInt(i -> i).toArray();
        }
        return new int[0];
    }
}

（全文完）