力扣第 326 场周赛

比赛时间 2023-01-01。本场周赛国服共 1722 人 AK。

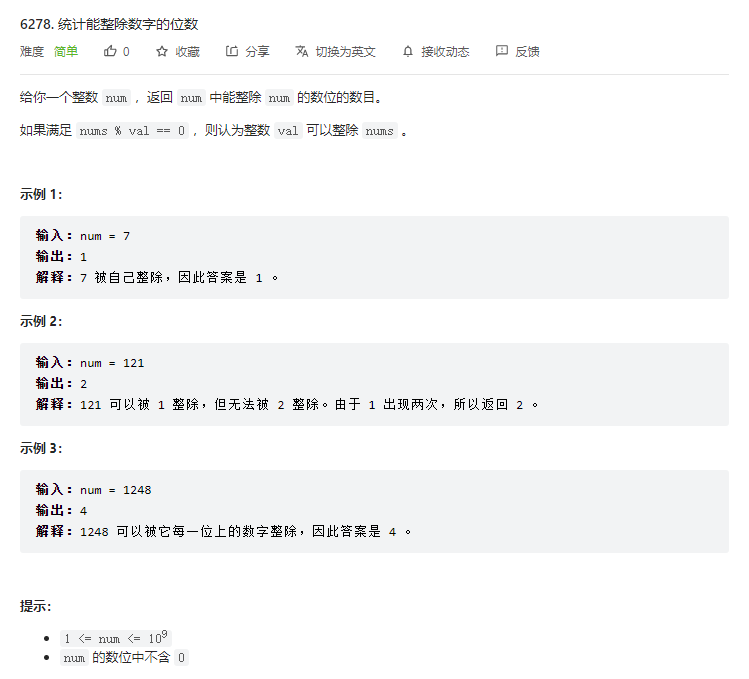
T1. 统计能整除数字的位数（3 分）

解题思路

模拟。

时间复杂度：O(n)。

参考代码

class Solution {
    public int countDigits(int num) {
        int cnt = 0;
        int n = num;
        while (n > 0) {
            int val = n % 10;
            if (num % val == 0) {
                cnt++;
            }
            n /= 10;
        }
        return cnt;
    }
}

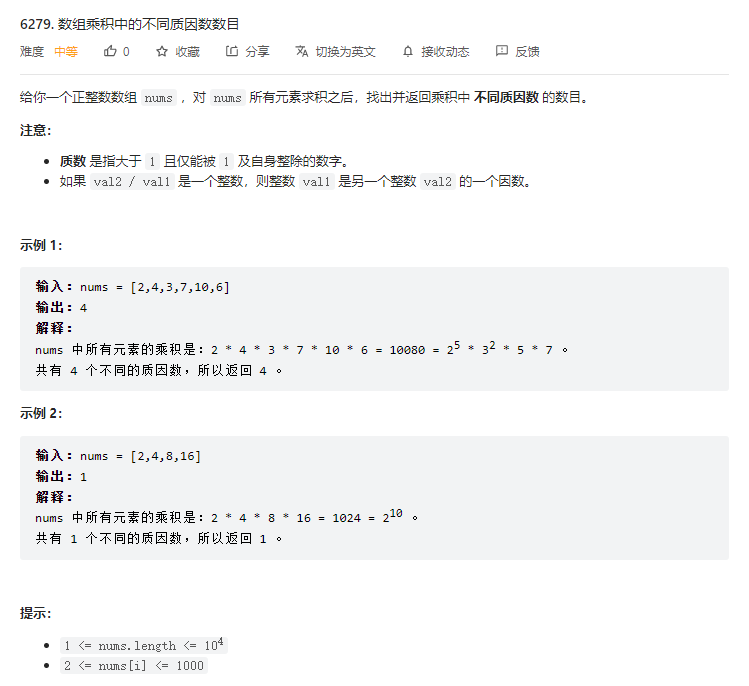
T2. 数组乘积中的不同质因数数目（4 分）

解题思路

分解质因数。

时间复杂度：O(n√n)。

参考代码

class Solution {
    public int distinctPrimeFactors(int[] nums) {
        Set<Integer> primeFactorSet = new HashSet<>();
        for (int num : nums) {
            for (int i = 2; i * i <= num; i++) {
                // 如果 i 能够整除 N，说明 i 为 N 的一个质因子。
                if (num % i == 0) {
                    while (num % i == 0) {
                        num /= i;
                    }
                    primeFactorSet.add(i);
                }
            }
            // 说明再经过操作之后 N 留下了一个素数
            if (num != 1) {
                primeFactorSet.add(num);
            }
        }
        return primeFactorSet.size();
    }
}

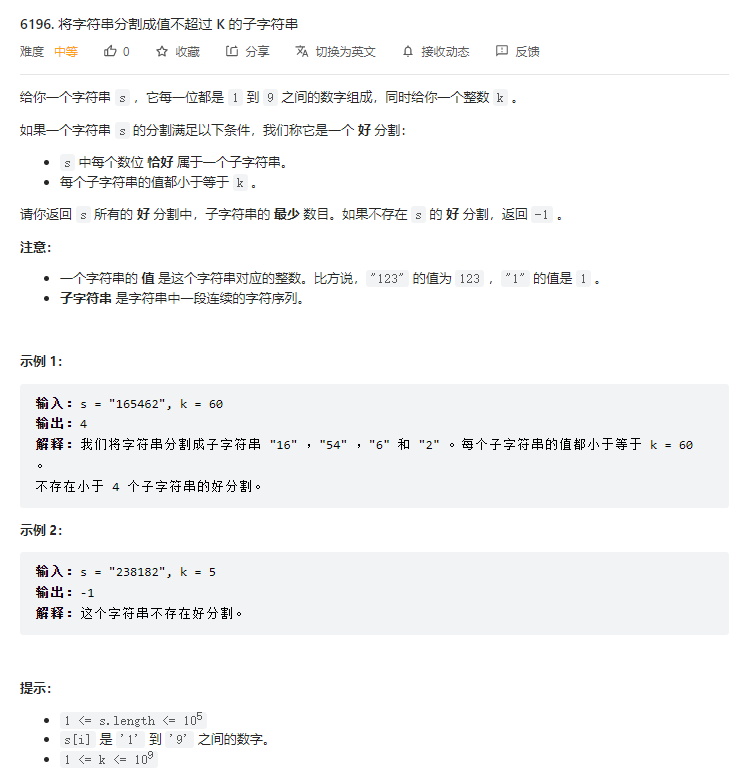
T3. 将字符串分割成值不超过 K 的子字符串（5 分）

解题思路

贪心 + 枚举。不得不分时才分。

时间复杂度：O(n)。

参考代码

class Solution {
    public int minimumPartition(String s, int k) {
        int cnt = 0;
        long num = 0L;
        for (char ch : s.toCharArray()) {
            if (num * 10 + (ch - '0') <= k) {
                num = num * 10 + (ch - '0');
            } else {
                cnt++;
                num = (ch - '0');
                if (num > k) {
                    return -1;
                }
            }
        }
        if (num <= k) {
            cnt++;
        } else {
            return -1;
        }
        return cnt;
    }
}

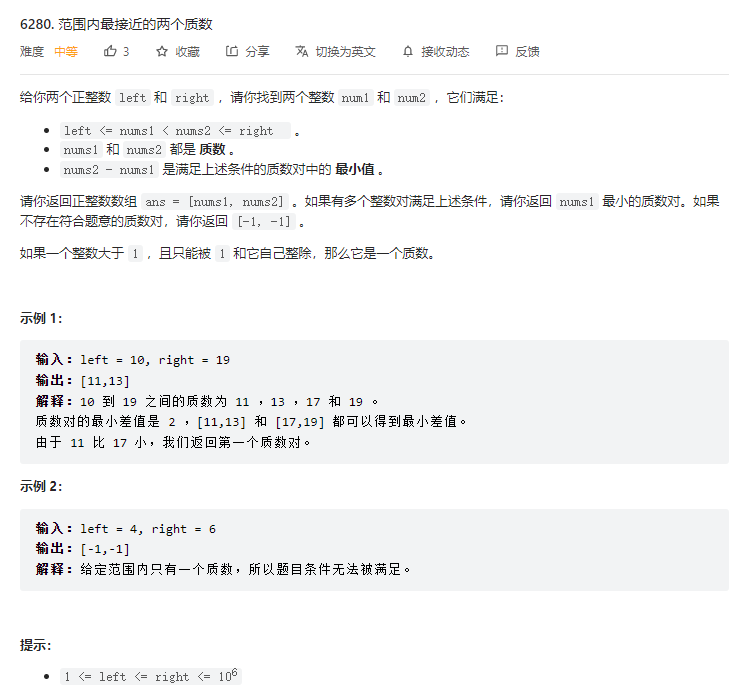
T4. 范围内最接近的两个质数（5 分）

解题思路

素数筛 + 枚举。这里使用时间复杂度 O(n) 的线性筛。

时间复杂度：O(n)。

参考代码

class Solution {
    private static final int MAX_N = (int) (1e6 + 1);
    private static List<Integer> primes;

    public int[] closestPrimes(int left, int right) {
        if (primes == null) {
            primes = new ArrayList<>();
            boolean[] isPrime = new boolean[MAX_N];
            Arrays.fill(isPrime, true);
            for (int i = 2; i < MAX_N; i++) {
                if (isPrime[i]) {
                    primes.add(i);
                }
                for (int j = 0; j < primes.size() && i * primes.get(j) < MAX_N; j++) {
                    isPrime[i * primes.get(j)] = false;
                    if (i % primes.get(j) == 0) {
                        break;
                    }
                }
            }
        }

        int[] ans = {-1, -1};
        // n = 1e6, sz = 78498
        int sz = primes.size();
        int min = MAX_N;
        for (int i = 1; i < sz; i++) {
            int pre = primes.get(i - 1);
            int cur = primes.get(i);
            if (pre >= left && cur <= right) {
                if (min > cur - pre) {
                    min = cur - pre;
                    ans = new int[]{pre, cur};
                }
            }
        }
        return ans;
    }
}

（全文完）