力扣第 334 场周赛

比赛时间 2023-02-26。本场周赛国服共 360 人 AK。

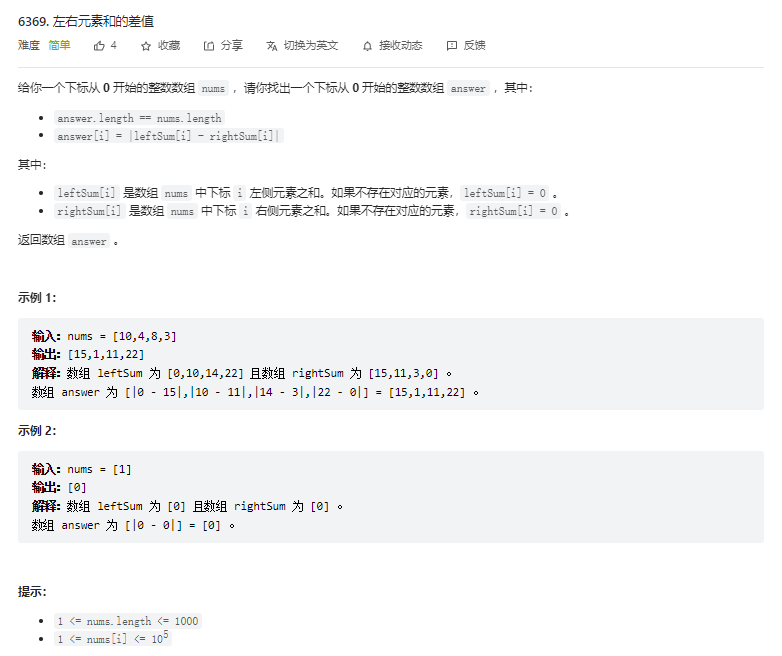
T1. 左右元素和的差值（3 分）

解题思路

前缀和。leftSum[i] = [0,i-1] 区间和；rightSum[i] = [i+1,n-1] 区间和。

时间复杂度：O(n)。

参考代码

class Solution {
    public int[] leftRigthDifference(int[] nums) {
        int n = nums.length;

        // 前缀和
        int[] preSum = new int[n + 1];
        for (int i = 0; i < n; i++) {
            preSum[i + 1] = preSum[i] + nums[i];
        }

        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            int leftSum = preSum[i];
            int rightSum = preSum[n] - preSum[i + 1];
            ans[i] = Math.abs(leftSum - rightSum);
        }
        return ans;
    }
}

T2. 找出字符串的可整除数组（4 分）

解题思路

贪心。如果 x 可以整除 m，那么 x * 10 也必然可以整除 m。取余之后不影响结果。

时间复杂度：O(n)。

参考代码

class Solution {
    public int[] divisibilityArray(String word, int m) {
        int n = word.length();

        long x = 0L;
        int[] div = new int[n];
        for (int i = 0; i < n; i++) {
            x = x * 10 + (word.charAt(i) - '0');
            if (x % m == 0) {
                div[i] = 1;
            }
            x %= m;
        }
        return div;
    }
}

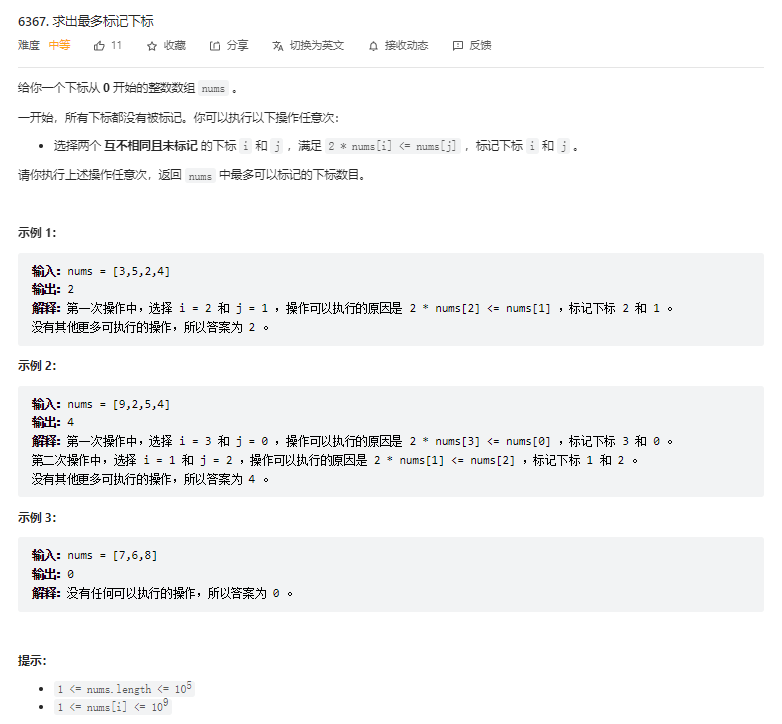
T3. 求出最多标记下标（5 分）

解题思路

二分 + 贪心。二分查找转化为判定问题：是否可以构造 k 对匹配。根据贪心：当最小 k 个数和最大 k 个数一一匹配时，配对数最大。

时间复杂度：O(nlogn)。

参考代码

class Solution {
    public int maxNumOfMarkedIndices(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);

        int left = 1;
        int right = n / 2 + 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            // 边界二分 F, F,..., F, [T, T,..., T]
            // ----------------------^
            if (!checkMid(nums, mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return (left - 1) * 2;
    }

    // 是否可以构造 k 对匹配（最小 k 个数和最大 k 个数 一一匹配）
    private boolean checkMid(int[] nums, int k) {
        int n = nums.length;
        for (int i = 0; i < k; i++) {
            if (nums[i] * 2 > nums[n - k + i]) {
                return false;
            }
        }
        return true;
    }
}

T4. 在网格图中访问一个格子的最少时间（6 分）

解题思路

堆优化 Dijkstra 最短路。

首先，特判 grid[0][1] > 1 && grid[1][0] > 1 情况，此时“困毙”（“困毙”：中国象棋术语。指轮到行棋的一方，棋子没有被将军，但所有棋子被困在原地无子可动，即被困毙）。

否则，可以通过“走闲”来凑时间，总能到达终点（“走闲”：中国象棋术语。表示行棋方无意进攻，走闲是用于等待时机或用于防守的战术）。

注意时间奇偶性：因“走闲”一次时间 +2。如：3->5 需要 t+2+1；3->6 同样需要 t+2+1。

最后 dijkstra 求最短路即可。

时间复杂度：O(mnlogmn)。

参考代码

class Solution {
    private static final int[][] DIRECTIONS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public int minimumTime(int[][] grid) {
        int M = grid.length;
        int N = grid[0].length;

        // “困毙”
        if (grid[0][1] > 1 && grid[1][0] > 1) {
            return -1;
        }

        PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o[2]));
        queue.add(new int[]{0, 0, 0});
        boolean[][] visited = new boolean[M][N];
        // 到达 grid[i][j] 所需的最少时间
        int[][] t = new int[M][N];
        for (int i = 0; i < M; i++) {
            Arrays.fill(t[i], Integer.MAX_VALUE);
        }
        t[0][0] = 0;
        while (!queue.isEmpty()) {
            int[] tuple = queue.remove();
            int cx = tuple[0], cy = tuple[1], ct = tuple[2];
            if (visited[cx][cy]) {
                continue;
            }
            visited[cx][cy] = true;

            for (int[] dir : DIRECTIONS) {
                int nx = cx + dir[0];
                int ny = cy + dir[1];
                if (nx >= 0 && nx < M && ny >= 0 && ny < N) {
                    // “走闲”
                    int nt = ct + 1 + (Math.max(0, grid[nx][ny] - ct) / 2 * 2);
                    if (t[nx][ny] > nt) {
                        t[nx][ny] = nt;
                        queue.add(new int[]{nx, ny, nt});
                    }
                }
            }
        }
        return t[M - 1][N - 1];
    }
}

（全文完）