力扣第 340 场周赛

比赛时间 2023-04-09。本场周赛国服共 298 人 AK。

T1. 对角线上的质数（3 分）

解题思路

线性筛 + 模拟。

线性筛预处理 4e6 内所有质数。再在 O(1) 时间内快速判断某个数是否为质数，若是质数，统计最大值。

时间复杂度：O(4e6 + n)。

参考代码

class Solution {
    private static final int MAX_N = (int) 4e6 + 1;
    private static Set<Integer> primeSet;

    public int diagonalPrime(int[][] nums) {
        if (primeSet == null) {
            List<Integer> primes = new ArrayList<>();
            boolean[] isPrime = new boolean[MAX_N];
            Arrays.fill(isPrime, true);
            for (int i = 2; i < MAX_N; i++) {
                if (isPrime[i]) {
                    primes.add(i);
                }
                for (int j = 0; j < primes.size() && i * primes.get(j) < MAX_N; j++) {
                    isPrime[i * primes.get(j)] = false;
                    if (i % primes.get(j) == 0) {
                        break;
                    }
                }
            }
            primeSet = new HashSet<>(primes);
        }

        int n = nums.length;
        int max = 0;
        for (int i = 0; i < n; i++) {
            if (primeSet.contains(nums[i][i])) {
                max = Math.max(max, nums[i][i]);
            }
            if (primeSet.contains(nums[i][n - 1 - i])) {
                max = Math.max(max, nums[i][n - 1 - i]);
            }
        }
        return max;
    }
}

T2. 等值距离和（4 分）

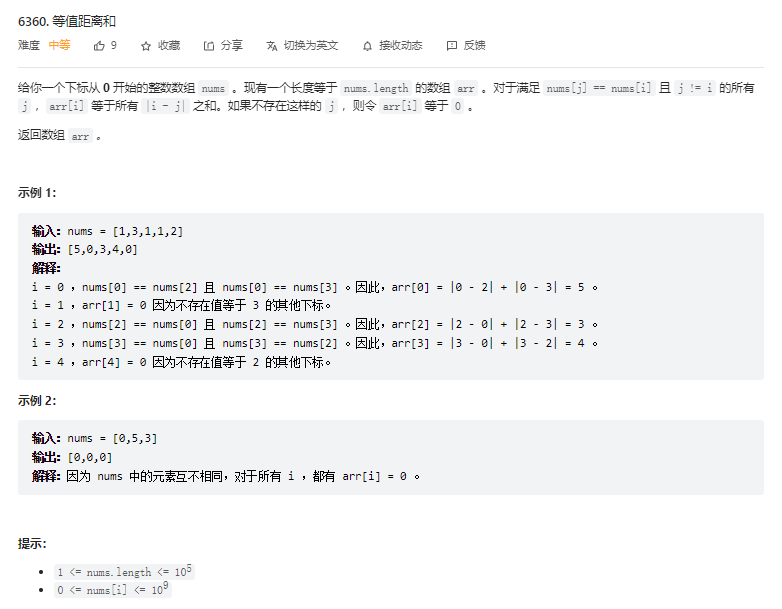
解题思路

相同元素分组 + 观察变化量。

据说是 2121 原题，但已经不记得了，又重新推了一遍规律。

时间复杂度：O(n)。

参考代码

class Solution {
    public long[] distance(int[] nums) {
        int n = nums.length;
        Map<Integer, List<Integer>> idxListMap = new HashMap<>();
        for (int i = 0; i < n; i++) {
            idxListMap.computeIfAbsent(nums[i], key -> new ArrayList<>()).add(i);
        }

        long[] arr = new long[n];
        for (List<Integer> ids : idxListMap.values()) {
            int sz = ids.size();
            if (sz == 1) continue;

            long sum = 0L;
            for (int i = 1; i < sz; i++) {
                sum += ids.get(i) - ids.get(0);
            }
            arr[ids.get(0)] = sum;

            for (int i = 1; i < sz; i++) {
                long d1 = ids.get(i) - ids.get(i - 1);
                sum -= (sz - 1L - i) * d1;
                sum += (i - 1L) * d1;
                arr[ids.get(i)] = sum;
            }
        }
        return arr;
    }
}

T3. 最小化数对的最大差值（5 分）

解题思路

二分查找 + 贪心。

排序后，基于贪心写 check 函数。

时间复杂度：O(nlogn + nlogU)。其中 n = nums.length, U = max(nums[i]) - min(nums[i])。

参考代码

class Solution {
    public int minimizeMax(int[] nums, int p) {
        Arrays.sort(nums);
        int max = 0;
        for (int i = 1; i < nums.length; i++) {
            max = Math.max(max, nums[i] - nums[i - 1]);
        }

        int left = 0;
        int right = max;
        while (left < right) {
            int mid = left + (right - left) / 2;
            // 边界二分 F, F,..., F, [T, T,..., T]
            // ----------------------^
            if (checkMid(nums, p, mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

    private boolean checkMid(int[] nums, int p, int mid) {
        int cnt = 0;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] - nums[i - 1] <= mid) {
                cnt++;
                i++;
            }
        }
        return cnt >= p;
    }
}

T4. 网格图中最少访问的格子数（6 分）

解题思路

BFS + 平衡树剪枝。

上周周赛 T4 的二维版本。

时间复杂度：O(mnlog(mn))。

参考代码

class Solution {
    public int minimumVisitedCells(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;

        // y->[x]
        List<TreeSet<Integer>> unVisitedXs = new ArrayList<>();
        for (int j = 0; j < n; j++) {
            TreeSet<Integer> unVisitedX = new TreeSet<>();
            for (int i = 0; i < m; i++) unVisitedX.add(i);
            unVisitedXs.add(unVisitedX);
        }
        // x->[y]
        List<TreeSet<Integer>> unVisitedYs = new ArrayList<>();
        for (int i = 0; i < m; i++) {
            TreeSet<Integer> unVisitedY = new TreeSet<>();
            for (int j = 0; j < n; j++) unVisitedY.add(j);
            unVisitedYs.add(unVisitedY);
        }

        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[]{0, 0, 1});
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                int[] tuple = queue.remove();
                int cx = tuple[0], cy = tuple[1], cstep = tuple[2];
                if (cx == m - 1 && cy == n - 1) {
                    return cstep;
                }

                int yDown = cy + 1;
                int yUp = Math.min(grid[cx][cy] + cy, n - 1);
                TreeSet<Integer> unVisY = unVisitedYs.get(cx);
                for (Integer ny = unVisY.ceiling(yDown); ny != null && ny <= yUp; ny = unVisY.higher(ny)) {
                    queue.add(new int[]{cx, ny, cstep + 1});
                    unVisY.remove(ny);
                }

                int xDown = cx + 1;
                int xUp = Math.min(grid[cx][cy] + cx, m - 1);
                TreeSet<Integer> unVisX = unVisitedXs.get(cy);
                for (Integer nx = unVisX.ceiling(xDown); nx != null && nx <= xUp; nx = unVisX.higher(nx)) {
                    queue.add(new int[]{nx, cy, cstep + 1});
                    unVisX.remove(nx);
                }
            }
        }
        return -1;
    }
}

（全文完）