力扣第 449 场周赛
2025年6月15日大约 4 分钟
力扣第 449 场周赛
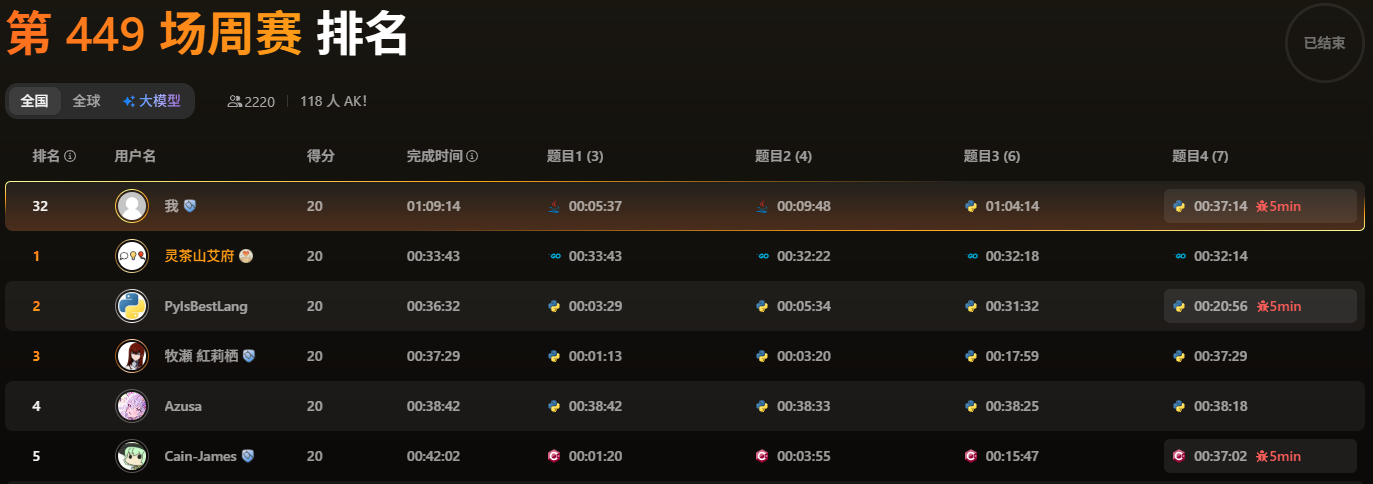
比赛时间 2025-05-11。本场周赛国服共 118 人 AK。
围棋是一门深奥的学问
越是强大的人 就越会认真思考 败退时的姿态
如何承认失败 如何投子认负 这都十分重要
没有人会责怪 认真挑战之后认输的人
也不会嘲笑他临阵脱逃
相反 还会称赞他们适时而退
因为大家都知道 这个人 直到最后 都渴望着胜利——《强风吹拂》
T1. 不同字符数量最多为 K 时的最少删除数(3 分)

解题思路
贪心。
时间复杂度:O(ClogC)。其中 C = 26。
参考代码
class Solution {
public int minDeletion(String s, int k) {
int[] cnt = new int[26];
for (char c : s.toCharArray()) {
cnt[c - 'a']++;
}
Arrays.sort(cnt);
int ans = s.length();
for (int i = 0; i < k; i++) {
int j = 25 - i;
ans -= cnt[j];
}
return ans;
}
}T2. 等和矩阵分割 I(4 分)

解题思路
二维前缀和 + 枚举。
时间复杂度:O(mn)。
参考代码
class Solution {
private long[][] ps2d;
public boolean canPartitionGrid(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
ps2d = new long[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
ps2d[i][j] = ps2d[i - 1][j] + ps2d[i][j - 1] - ps2d[i - 1][j - 1] + grid[i - 1][j - 1];
}
}
if (ps2d[m][n] % 2 != 0) return false;
long target = ps2d[m][n] / 2;
for (int i = 0; i < m; i++) {
if (sumRegion(0, 0, i, n - 1) == target) return true;
}
for (int j = 0; j < n; j++) {
if (sumRegion(0, 0, m - 1, j) == target) return true;
}
return false;
}
// 求 [r1,c1] 到 [r2,c2] 的累加和
private long sumRegion(int r1, int c1, int r2, int c2) {
return ps2d[r2 + 1][c2 + 1] - ps2d[r2 + 1][c1] - ps2d[r1][c2 + 1] + ps2d[r1][c1];
}
}T3. 图中边值的最大和(6 分)
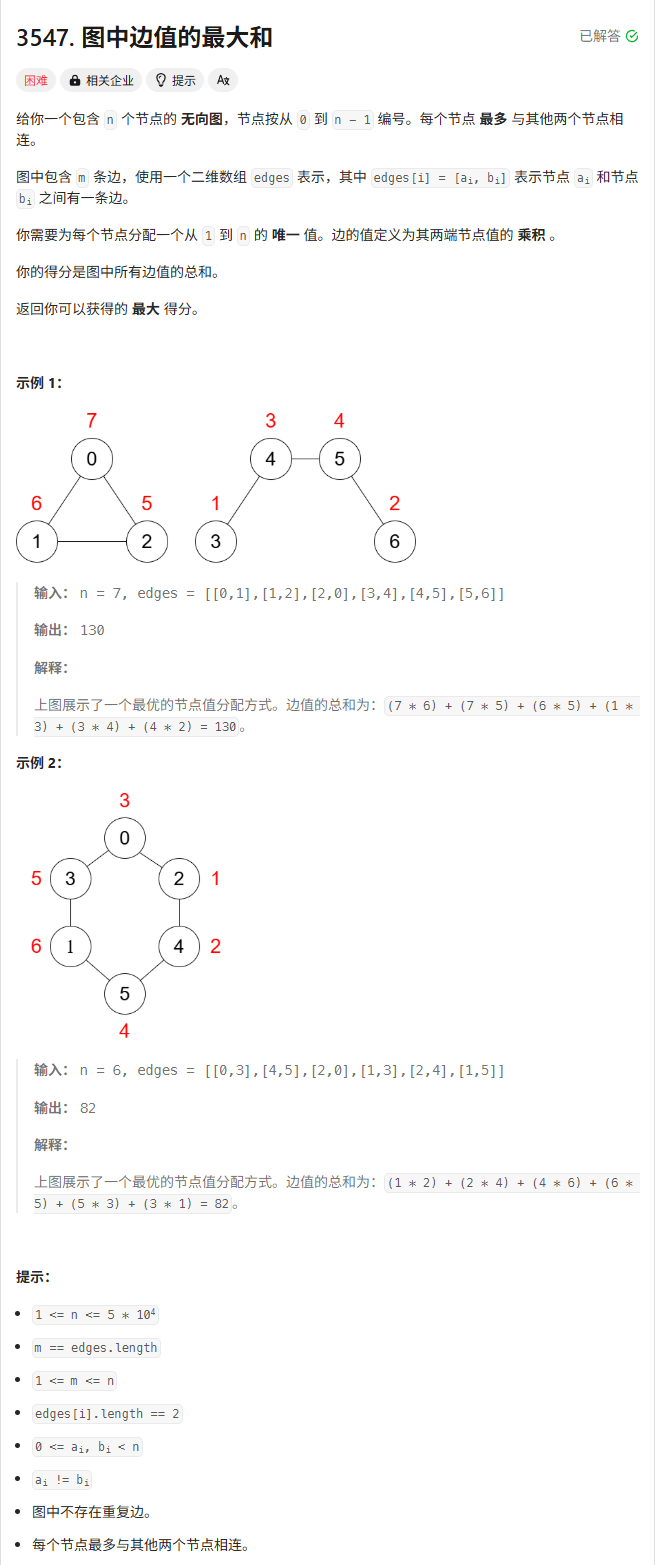
解题思路
因为题目出错不知道起什么标题。
评论区有人给出了如下数据:
11
[[0,1],[1,2],[2,3],[5,6],[6,7]]这个数据预期结果是 366,但实际上可以构造 9-11-10-7 和 5-8-6 两条链,算出结果是 367。
参考代码
class Solution3547 {
record Component(int isCycle, int size) {
}
private List<Integer>[] g;
private boolean[] vis;
private int cntV, cntE;
public long maxScore(int n, int[][] edges) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (int[] e : edges) {
g[e[0]].add(e[1]);
g[e[1]].add(e[0]);
}
List<Component> components = new ArrayList<>();
vis = new boolean[n];
for (int i = 0; i < n; i++) {
if (!vis[i]) {
cntV = 0;
cntE = 0;
dfs(i);
int isCycle = cntE / 2 == cntV ? 1 : 0;
components.add(new Component(isCycle, cntV));
}
}
components.sort((a, b) -> {
if (a.isCycle == b.isCycle) {
return Integer.compare(b.size, a.size);
}
return Integer.compare(b.isCycle, a.isCycle);
});
int num = n;
long totalScore = 0;
for (Component comp : components) {
int k = comp.size;
boolean isCycle = comp.isCycle == 1;
// 构造排列
Deque<Integer> dq = new ArrayDeque<>();
boolean left = true;
for (int i = 0; i < k; i++) {
if (left) {
dq.addFirst(num);
} else {
dq.addLast(num);
}
num--;
left = !left;
}
List<Integer> arranged = new ArrayList<>(dq);
// 计算分数
if (isCycle) {
long score = 0;
for (int i = 0; i < k; i++) {
int next = (i + 1) % k;
score += (long) arranged.get(i) * arranged.get(next);
}
totalScore += score;
} else {
long score = 0;
for (int i = 0; i < k - 1; i++) {
score += (long) arranged.get(i) * arranged.get(i + 1);
}
totalScore += score;
}
}
return totalScore;
}
private void dfs(int x) {
vis[x] = true;
cntV++;
cntE += g[x].size();
for (int y : g[x]) {
if (vis[y]) continue;
dfs(y);
}
}
}T4. 等和矩阵分割 II(7 分)

解题思路
二维前缀和 + 枚举 + 分类讨论。
时间复杂度:O(mn)。
参考代码
class Solution {
private long[][] ps2d;
public boolean canPartitionGrid(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
ps2d = new long[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
ps2d[i][j] = ps2d[i - 1][j] + ps2d[i][j - 1] - ps2d[i - 1][j - 1] + grid[i - 1][j - 1];
}
}
long tot = ps2d[m][n];
for (int i = 0; i + 1 < m; i++) {
long upSum = sumRegion(0, 0, i, n - 1);
// 不挖
if (tot % 2 == 0 && upSum == tot / 2) return true;
// 上部挖
long[] rm = {grid[0][0], grid[0][n - 1], grid[i][0], grid[i][n - 1]};
for (long v : rm) {
if ((tot - v) % 2 == 0 && upSum - v == (tot - v) / 2) return true;
}
// 下部挖
rm = new long[]{grid[i + 1][0], grid[i + 1][n - 1], grid[m - 1][0], grid[m - 1][n - 1]};
for (long v : rm) {
if ((tot - v) % 2 == 0 && upSum == (tot - v) / 2) return true;
}
}
for (int j = 0; j + 1 < n; j++) {
// 不挖
long leftSum = sumRegion(0, 0, m - 1, j);
if (tot % 2 == 0 && leftSum == tot / 2) return true;
// 左部挖
long[] rm = new long[]{grid[0][0], grid[0][j], grid[m - 1][0], grid[m - 1][j]};
for (long v : rm) {
if ((tot - v) % 2 == 0 && leftSum - v == (tot - v) / 2) return true;
}
// 右部挖
rm = new long[]{grid[0][j + 1], grid[0][n - 1], grid[m - 1][j + 1], grid[m - 1][n - 1]};
for (long v : rm) {
if ((tot - v) % 2 == 0 && leftSum == (tot - v) / 2) return true;
}
}
return false;
}
// 求 [r1,c1] 到 [r2,c2] 的累加和
private long sumRegion(int r1, int c1, int r2, int c2) {
return ps2d[r2 + 1][c2 + 1] - ps2d[r2 + 1][c1] - ps2d[r1][c2 + 1] + ps2d[r1][c1];
}
}(全文完)