力扣第 454 场周赛

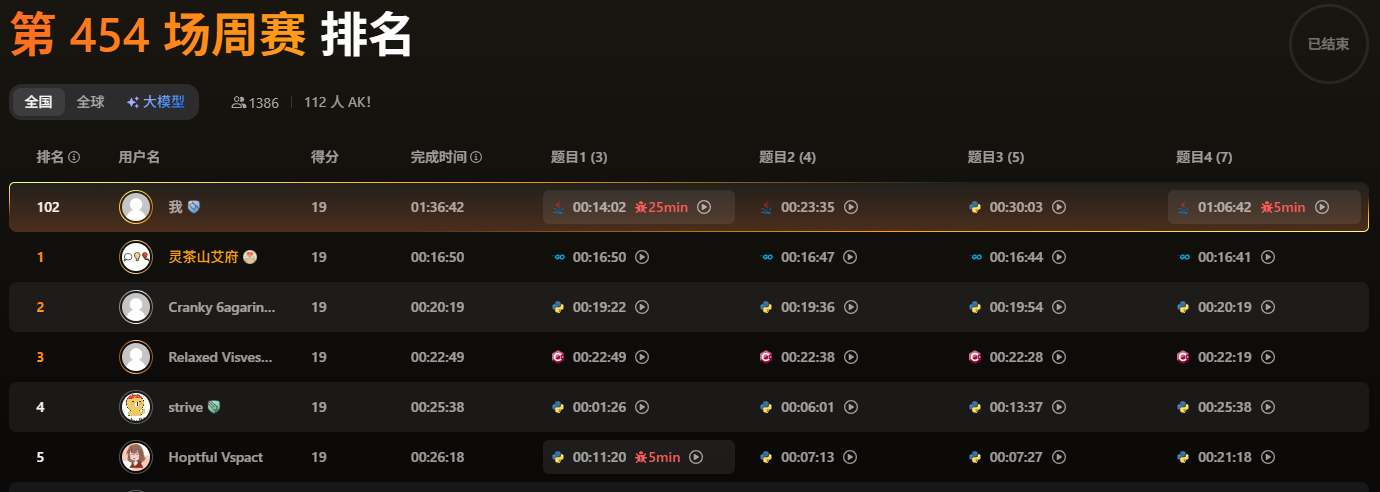
比赛时间 2025-06-15。本场周赛国服共 112 人 AK。

是日父亲节，祝愿天下所有的父亲们 身体健康 平安幸福！~

T1. 为视频标题生成标签（3 分）

解题思路

模拟。WA 了 5 次，细节是魔鬼。

时间复杂度：O(n)。

参考代码

class Solution {
    public String generateTag(String caption) {
        caption = ("#" + caption.strip()).toLowerCase();
        StringBuilder ans = new StringBuilder("#");
        for (int i = 1; i < caption.length(); i++) {
            char c = caption.charAt(i);
            if (c == ' ') continue;
            if (caption.charAt(i - 1) == ' ') {
                ans.append(Character.toUpperCase(c));
            } else {
                ans.append(c);
            }
        }
        return ans.substring(0, Math.min(100, ans.length()));
    }
}

T2. 统计特殊三元组（4 分）

解题思路

前后缀分解 + 枚举中间。

时间复杂度：O(n)。

参考代码

class Solution {
    private static final int MOD = (int) (1e9 + 7);

    public int specialTriplets(int[] nums) {
        int n = nums.length;
        int[] lcnt = new int[n];
        Map<Integer, Integer> cnt = new HashMap<>();
        for (int i = 0; i < n; i++) {
            lcnt[i] = cnt.getOrDefault(nums[i] * 2, 0);
            cnt.merge(nums[i], 1, Integer::sum);
        }

        int[] rcnt = new int[n];
        cnt.clear();
        for (int i = n - 1; i >= 0; i--) {
            rcnt[i] = cnt.getOrDefault(nums[i] * 2, 0);
            cnt.merge(nums[i], 1, Integer::sum);
        }

        long ans = 0;
        for (int i = 1; i + 1 < n; i++) {
            ans = (ans + (long) lcnt[i] * rcnt[i]) % MOD;
        }
        return (int) ans;
    }
}

T3. 子序列首尾元素的最大乘积（5 分）

解题思路

预处理后缀 + 贪心。

时间复杂度：O(n)。

参考代码

class Solution {
    private static final long INF = (long) 1e18;

    public long maximumProduct(int[] nums, int m) {
        int n = nums.length;
        if (m == 1) {
            long ans = 0;
            for (int x : nums) ans = Math.max(ans, (long) x * x);
            return ans;
        }
        int k = m - 1;

        int[] max_suffix = new int[n];
        int[] min_suffix = new int[n];
        max_suffix[n - 1] = nums[n - 1];
        min_suffix[n - 1] = nums[n - 1];

        for (int i = n - 2; i >= 0; i--) {
            max_suffix[i] = Math.max(nums[i], max_suffix[i + 1]);
            min_suffix[i] = Math.min(nums[i], min_suffix[i + 1]);
        }

        long candidate;
        long max_prod = -INF;
        for (int i = 0; i + k < n; i++) {
            int start = i + k;
            if (nums[i] >= 0) {
                candidate = (long) nums[i] * max_suffix[start];
            } else {
                candidate = (long) nums[i] * min_suffix[start];
            }
            max_prod = Math.max(max_prod, candidate);
        }

        return max_prod;
    }
}

T4. 树中找到带权中位节点（7 分）

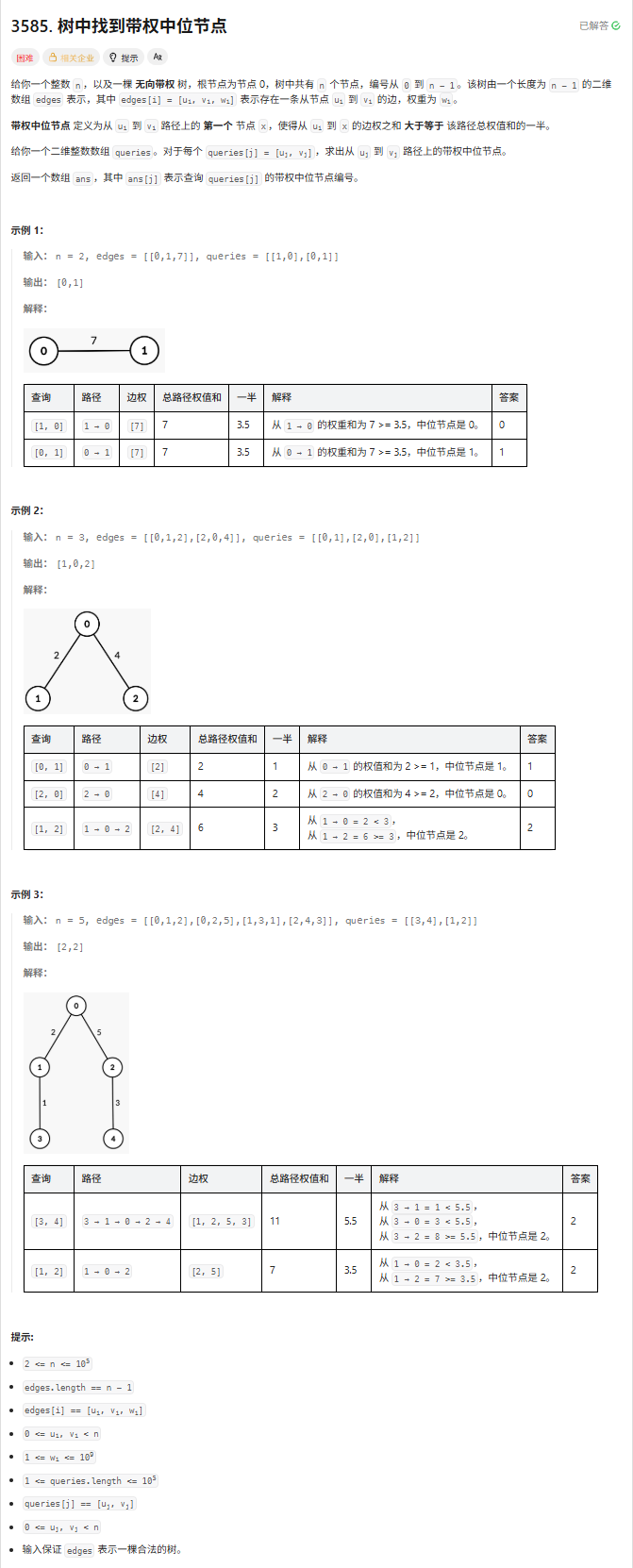
解题思路

最近公共祖先 LCA + 树上倍增。

先从 u 点倍增到 lca 点，若干未能得到答案，那么再从 lca 点倍增到 v 点（反向）。

时间复杂度：O((n+q)logn)。

参考代码

class Solution {
    private List<int[]>[] g;
    private int dfn;
    private int[][] nodes; // l, r
    private final int mx = 17;
    private int[][] pa;
    private int[] dep;
    private long[] sum_to_root;

    public int[] findMedian(int n, int[][] edges, int[][] queries) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int[] e : edges) {
            g[e[0]].add(new int[]{e[1], e[2]});
            g[e[1]].add(new int[]{e[0], e[2]});
        }
        dfn = 0;
        nodes = new int[n][2];
        pa = new int[n][mx];
        dep = new int[n];
        sum_to_root = new long[n];
        build(0, -1);
        for (int i = 0; i + 1 < mx; i++) {
            for (int v = 0; v < pa.length; v++) {
                int p = pa[v][i];
                if (p != -1) {
                    pa[v][i + 1] = pa[p][i];
                } else {
                    pa[v][i + 1] = -1;
                }
            }
        }

        int[] ans = new int[queries.length];
        for (int i = 0; i < queries.length; i++) {
            int u = queries[i][0], v = queries[i][1];
            long total = get_path_sum(u, v);
            int lcaNode = getLCA(u, v);
            int current1 = u;
            for (int k = mx - 1; k >= 0; k--) {
                int next_node = pa[current1][k];
                if (next_node == -1) continue;
                if (dep[next_node] < dep[lcaNode]) continue;
                if (2 * (sum_to_root[u] - sum_to_root[next_node]) < total) {
                    current1 = next_node;
                }
            }
            if (current1 != lcaNode) {
                ans[i] = pa[current1][0];
            } else {
                int candidate2 = v;
                for (int k = mx - 1; k >= 0; k--) {
                    int next_node = pa[candidate2][k];
                    if (next_node == -1) continue;
                    if (dep[next_node] <= dep[lcaNode]) continue;
                    if (2 * (sum_to_root[u] + sum_to_root[next_node] - 2 * sum_to_root[lcaNode]) >= total) {
                        candidate2 = next_node;
                    }
                }
                ans[i] = candidate2;
            }
        }
        return ans;
    }

    long get_path_sum(int u, int v) {
        int ancestor = getLCA(u, v);
        return sum_to_root[u] + sum_to_root[v] - 2 * sum_to_root[ancestor];
    }

    int build(int v, int fa) {
        dfn++;
        nodes[v][0] = dfn;
        pa[v][0] = fa;
        int sz = 1;
        for (int[] p : g[v]) {
            int w = p[0], wt = p[1];
            if (w != fa) {
                dep[w] = dep[v] + 1;
                sum_to_root[w] = sum_to_root[v] + wt;
                sz += build(w, v);
            }
        }
        nodes[v][1] = nodes[v][0] + sz - 1;
        return sz;
    }

    int uptoDep(int v, int d) {
        for (int k = dep[v] - d; k > 0; k &= k - 1) {
            v = pa[v][Integer.numberOfTrailingZeros(k)];
        }
        return v;
    }

    int getLCA(int v, int w) {
        if (dep[v] > dep[w]) {
            int tmp = v;
            v = w;
            w = tmp;
        }
        w = uptoDep(w, dep[v]);
        if (w == v) return v;
        for (int i = mx - 1; i >= 0; i--) {
            if (pa[v][i] != pa[w][i]) {
                v = pa[v][i];
                w = pa[w][i];
            }
        }
        return pa[v][0];
    }
}

（全文完）