LCCUP'22 力扣杯秋季编程大赛-战队赛/个人赛
LCCUP'22 力扣杯秋季编程大赛-战队赛/个人赛
战队赛
比赛时间 2022-10-07。感谢队友 @ming1ing、@kexp,喜提 Rank 112,超过了 97.1% 的队伍!
T1. 最小展台数量(2 分)

解题思路
贪心。对每天各类型的展台数取最大值,求和即可。
时间复杂度:O(n)。其中常数为 26。
参考代码
class Solution {
public int minNumBooths(String[] demand) {
int[] f = new int[26];
for (String s : demand) {
int[] f1 = new int[26];
for (char ch : s.toCharArray()) {
f1[ch - 'a']++;
}
for (int i = 0; i < 26; i++) {
f[i] = Math.max(f[i], f1[i]);
}
}
return Arrays.stream(f).sum();
}
}T2. 装饰树(4 分)
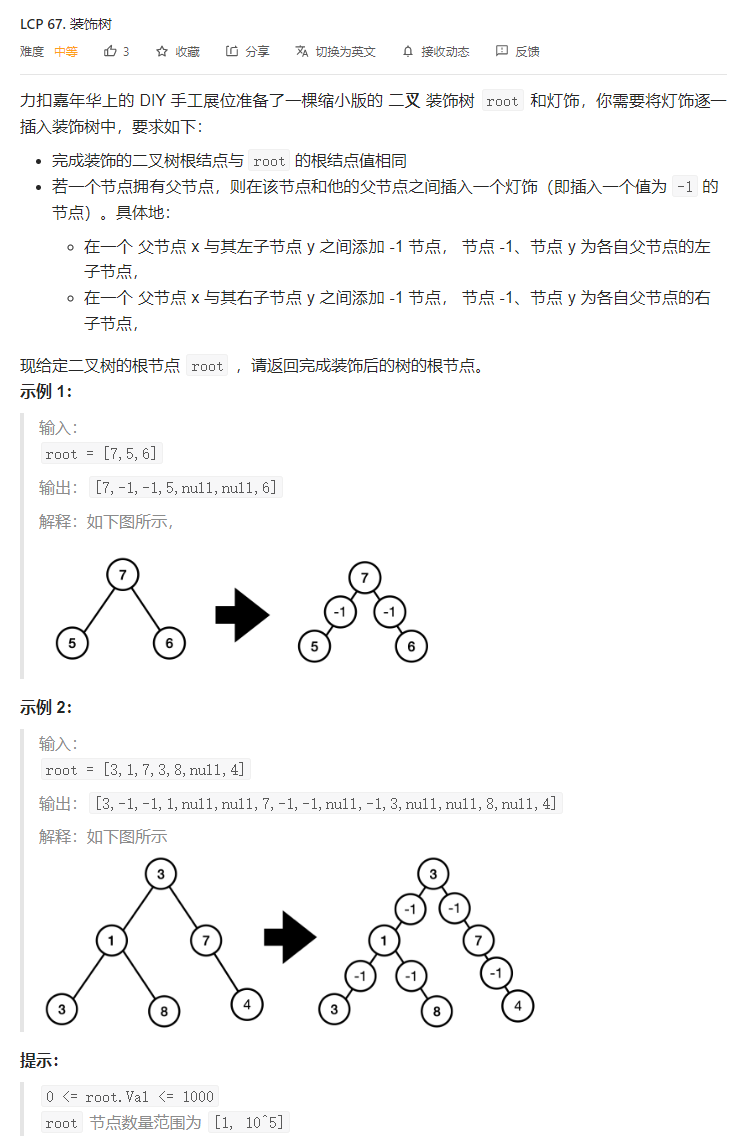
解题思路
二叉树递归。
时间复杂度:O(n)。
参考代码
class Solution {
public TreeNode expandBinaryTree(TreeNode root) {
if (root.left != null) {
TreeNode tmp = root.left;
root.left = new TreeNode(-1);
root.left.left = expandBinaryTree(tmp);
}
if (root.right != null) {
TreeNode tmp = root.right;
root.right = new TreeNode(-1);
root.right.right = expandBinaryTree(tmp);
}
return root;
}
}T3. 美观的花束(6 分)

解题思路
双指针。滑动窗口求每个下标贡献,累加即可。
时间复杂度:O(n)。
参考代码
class Solution {
private static final int MAX_N = (int) (1e5 + 5);
private static final int MOD = (int) (1e9 + 7);
public int beautifulBouquet(int[] flowers, int cnt) {
int len = flowers.length;
// 双指针
int left = 0;
int right = 0;
int[] cntArr = new int[MAX_N];
long res = 0;
while (right < len) {
cntArr[flowers[right]]++;
right++;
res += right - left;
res %= MOD;
while (right < len && cntArr[flowers[right]] == cnt) {
cntArr[flowers[left]]--;
left++;
}
}
return (int) res;
}
}T4. Hello LeetCode!(8 分)

解题思路
记忆化搜索。
字符串 helloleetcode 中,e 出现 4 次,l 出现 3 次,o 出现 2 次,h t c d 各出现 1 次,。因此状态共有 A = 5 * 4 * 3 * 2 * 2 * 2 * 2 = 960 种。
- 首先预处理出
costs[i][mask],表示从words[i]的单词里,获取字符状态为mask的最小代价。 - 再用记忆化搜索求获取到完整
helloleetcode的最小代价。
时间复杂度:O(n·A·m·2^m)。外加大量剪枝。
参考代码
class Solution {
private static final int INF = Integer.MAX_VALUE / 2;
private int n;
private List<Map<Node, Integer>> costs;
private List<Map<Node, Integer>> memo;
public int Leetcode(String[] words) {
n = words.length;
// 预处理每个单词的每种选择字母的方案所消耗的代币的最小值
costs = new ArrayList<>();
for (String word : words) {
Map<Node, Integer> costMap = new HashMap<>();
dfs(word, new Node(new int[7]), 0, costMap);
costs.add(costMap);
}
// 记忆化搜索
memo = new ArrayList<>();
for (int i = 0; i < n; i++) {
memo.add(new HashMap<>());
}
int res = dfs2(0, new Node(new int[7]));
return res == INF ? -1 : res;
}
private int dfs2(int i, Node mask) {
if (i == n) {
// inf 表示不合法,没有选完要求的字母
return mask.isFull() ? 0 : INF;
}
if (memo.get(i).containsKey(mask)) {
return memo.get(i).get(mask);
}
int res = INF;
for (Map.Entry<Node, Integer> entry : costs.get(i).entrySet()) {
Node add = entry.getKey();
int tot = entry.getValue();
// 剪枝
if (tot >= res) {
continue;
}
Node m = merge(mask, add);
if (m.isLess()) {
res = Math.min(res, tot + dfs2(i + 1, m));
}
}
if (!memo.get(i).containsKey(mask)) {
memo.get(i).put(mask, res);
}
return res;
}
private void dfs(String str, Node mask, int tot, Map<Node, Integer> costMap) {
if (!costMap.containsKey(mask) || costMap.get(mask) > tot) {
costMap.put(mask, tot);
}
for (int k = 0; k < str.length(); k++) {
char ch = str.charAt(k);
String nextStr = str.substring(0, k) + str.substring(k + 1);
int nextTot = tot + k * (str.length() - 1 - k);
for (int i = 0; i < Node.N; i++) {
// 可以选 ch
if (ch == Node.CHARS[i] && mask.cnt[i] < Node.LIMIT[i]) {
Node nextMask = new Node(mask.cnt);
nextMask.cnt[i]++;
dfs(nextStr, nextMask, nextTot, costMap);
break;
}
}
}
}
// 合并两种选择字母的方案
private Node merge(Node cur, Node add) {
Node res = new Node(cur.cnt);
for (int i = 0; i < Node.N; i++) {
res.cnt[i] += add.cnt[i];
}
return res;
}
private static class Node {
private static final int N = 7;
private static final char[] CHARS = {'e', 'l', 'o', 'h', 't', 'c', 'd'};
private static final int[] LIMIT = {4, 3, 2, 1, 1, 1, 1};
private final int[] cnt;
public Node(int[] tuple) {
cnt = new int[N];
System.arraycopy(tuple, 0, cnt, 0, N);
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (!(o instanceof Node node)) return false;
return Arrays.equals(cnt, node.cnt);
}
@Override
public int hashCode() {
return Arrays.hashCode(cnt);
}
boolean isFull() {
return Arrays.equals(cnt, LIMIT);
}
boolean isLess() {
for (int i = 0; i < N; i++) {
if (cnt[i] > LIMIT[i]) {
return false;
}
}
return true;
}
}
}T5. 沙地治理(9 分)
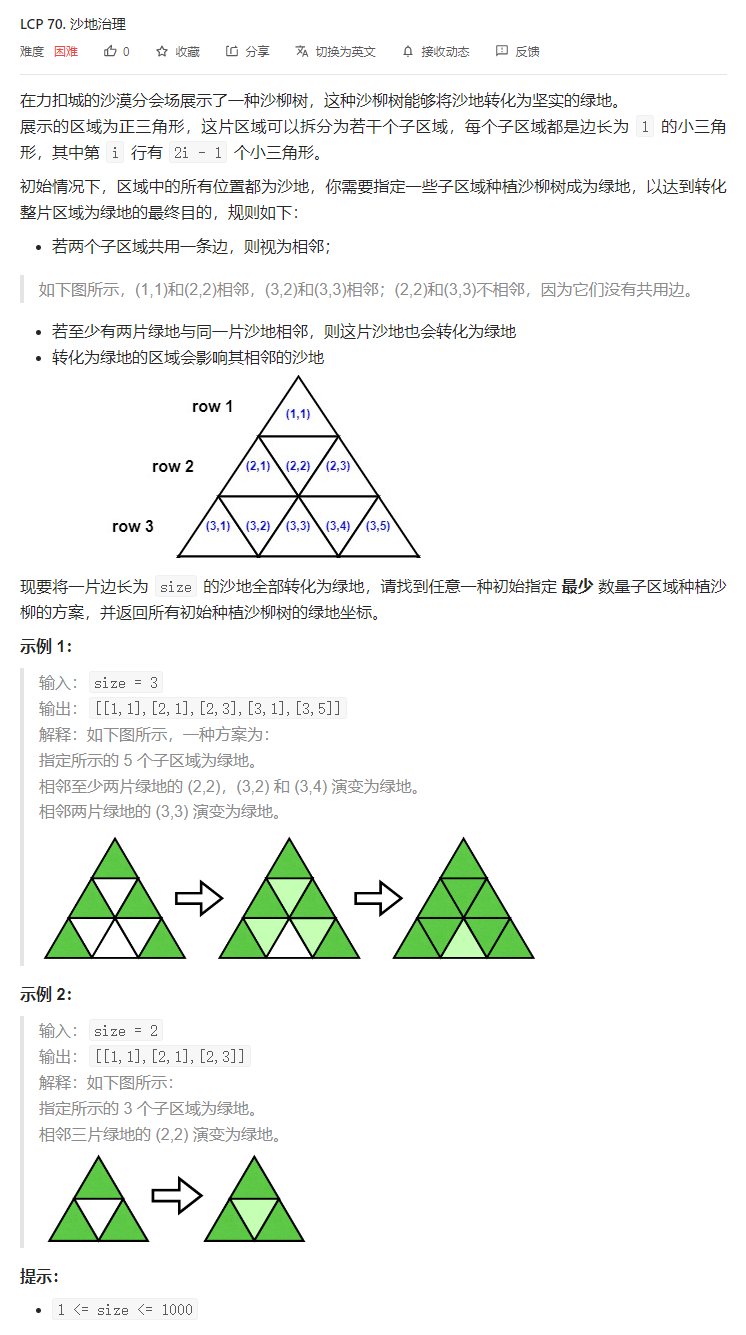
解题思路
构造题。找规律,没啥好说的。
一开始想法是覆盖两条边外加向下三角形即可。然后当 size=5 时不出意料 WA 了。
@ming1ing 提议多 WA 几次通过看更多的用例找规律。实践证明这招非常有用,WA 两发就能看出规律。如下图:
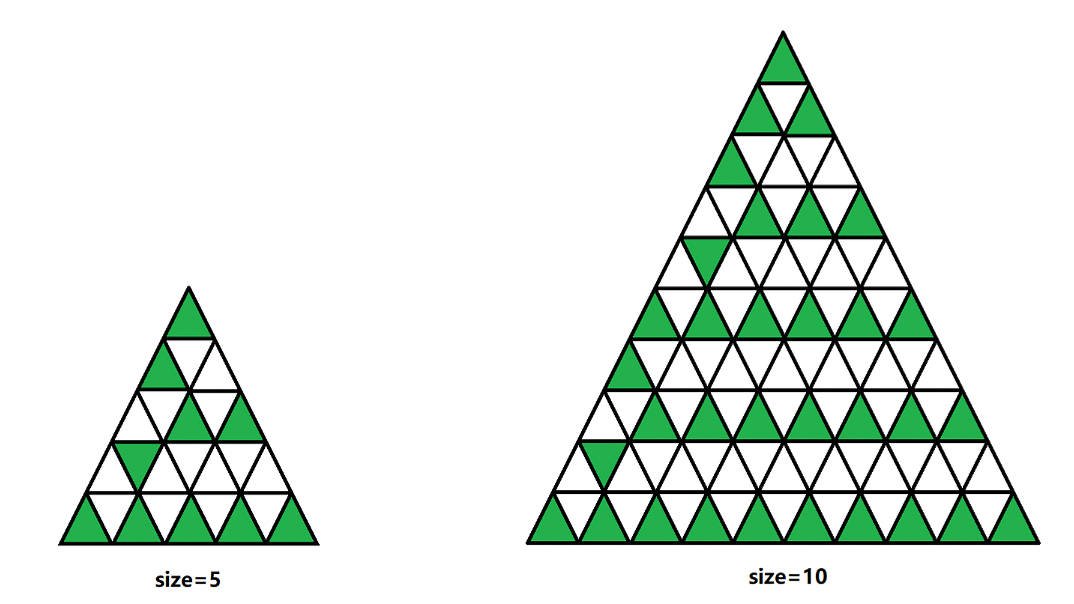
参考代码
class Solution {
public int[][] sandyLandManagement(int size) {
List<int[]> list = new ArrayList<>();
int k = 0;
list.add(new int[]{1, 1});
for (int i = size; i > 1; i--) {
if (k == 0) {
for (int j = 1; j <= i * 2 - 1; j += 2) {
list.add(new int[]{i, j});
}
} else if (k == 1) {
list.add(new int[]{i, 2});
} else if (k == 2) {
for (int j = 3; j <= i * 2 - 1; j += 2) {
list.add(new int[]{i, j});
}
} else {
list.add(new int[]{i, 1});
}
k = (k + 1) % 4;
}
return list.toArray(new int[list.size()][]);
}
}T6. 集水器(10 分)
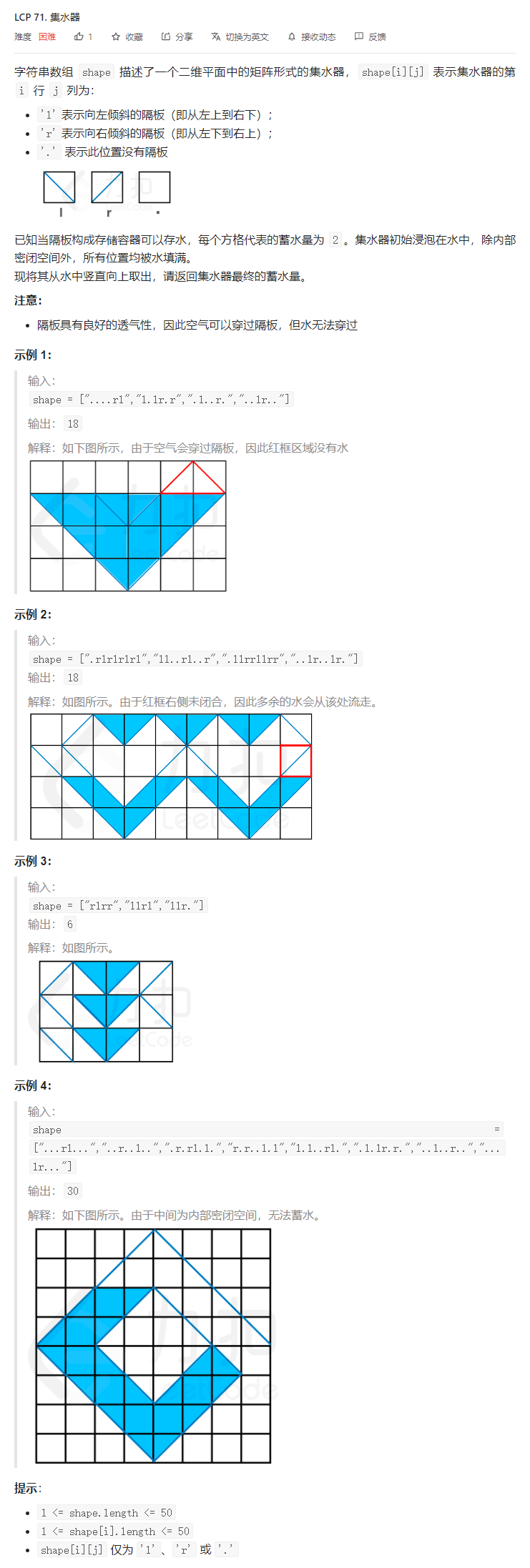
解题思路
并查集。
- 从下往上逐行使用并查集连通,不与外界连通的区域表示可能有水的(也有可能是完全密闭的)。
- 最后用并查集连通上边界,排除完全密闭的区域。求和即可。
时间复杂度:O(nm·logn)。其中路径压缩并查集最坏时间复杂度为:O(logn)。
参考代码
class Solution {
public int reservoir(String[] shape) {
int M = shape.length;
int N = shape[0].length();
// 增加一层外边界
int[][] up = new int[M + 2][N + 2];
int[][] down = new int[M + 2][N + 2];
int[][] left = new int[M + 2][N + 2];
int[][] right = new int[M + 2][N + 2];
// 共 4·M·N 个点 映射到 [0, id)
int id = 0;
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
up[i][j] = id++;
right[i][j] = id++;
left[i][j] = id++;
down[i][j] = id++;
}
}
// 左右边界连超级汇点 id
for (int i = 1; i <= M; i++) {
right[i][0] = id;
left[i][N + 1] = id;
}
// 下边界连超级汇点 id
for (int j = 1; j <= N; j++) {
up[M + 1][j] = id;
}
boolean[] mayWater = new boolean[id + 1];
// 并查集
DSU dsu = new DSU(id + 1);
// 从下往上枚举
for (int i = M; i >= 1; i--) {
// 连通左右
for (int j = 0; j <= N; j++) {
dsu.union(right[i][j], left[i][j + 1]);
}
// 连通上下
for (int j = 1; j <= N; j++) {
dsu.union(down[i][j], up[i + 1][j]);
}
// 连通格子内部
for (int j = 1; j <= N; j++) {
char ch = shape[i - 1].charAt(j - 1);
if (ch == '.') {
dsu.union(up[i][j], down[i][j]);
dsu.union(up[i][j], left[i][j]);
dsu.union(up[i][j], right[i][j]);
} else if (ch == 'l') {
dsu.union(left[i][j], down[i][j]);
dsu.union(up[i][j], right[i][j]);
} else {
dsu.union(left[i][j], up[i][j]);
dsu.union(down[i][j], right[i][j]);
}
}
// 不连通表示可能有水
for (int j = 1; j <= N; j++) {
mayWater[up[i][j]] = (dsu.find(up[i][j]) != dsu.find(id));
mayWater[down[i][j]] = (dsu.find(down[i][j]) != dsu.find(id));
mayWater[left[i][j]] = (dsu.find(left[i][j]) != dsu.find(id));
mayWater[right[i][j]] = (dsu.find(right[i][j]) != dsu.find(id));
}
}
// 第一行连超级汇点
for (int j = 1; j <= N; j++) {
dsu.union(up[1][j], id);
}
// 统计数量
int res = 0;
for (int i = 0; i < id; i++) {
// 不在闭合区域内可能有水
if (mayWater[i] && dsu.find(i) == dsu.find(id)) {
res++;
}
}
return res / 2;
}
private static class DSU {
// 父节点数组/祖先数组
int[] fa;
// 初始化
public DSU(int n) {
fa = new int[n];
for (int i = 0; i < n; i++) {
fa[i] = i;
}
}
// 查找
int find(int x) {
// 路径压缩
if (x != fa[x]) {
fa[x] = find(fa[x]);
}
return fa[x];
}
// 合并
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) {
return;
}
fa[rootQ] = rootP;
}
}
}个人赛
历史上参加的三次个人赛,时间全在“月末周六”(2021-09-11、2022-04-16、2022-09-24)。意难平,只能简单做个签到题。
T1. 气温变化趋势(2 分)
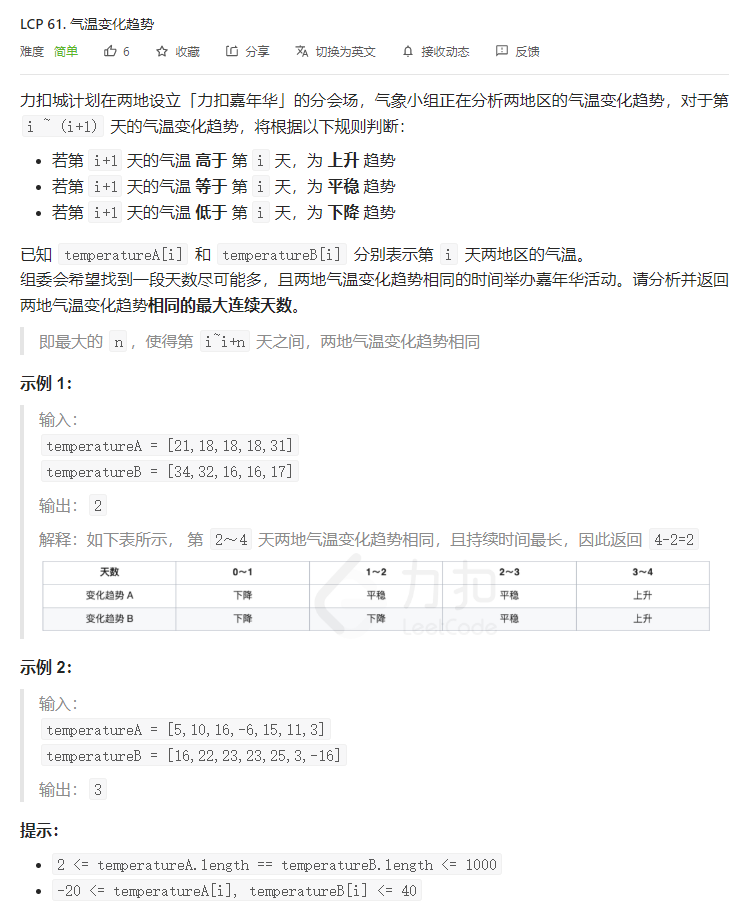
解题思路
枚举。令 isEqual[i] 表示第 i 天两地气温变化趋势是否相同。求最大连续区间即可。
时间复杂度:O(n)。
参考代码
class Solution {
public int temperatureTrend(int[] temperatureA, int[] temperatureB) {
int n = temperatureA.length;
boolean[] isEqual = new boolean[n];
for (int i = 1; i < n; i++) {
if ((temperatureA[i] - temperatureA[i - 1] > 0 && temperatureB[i] - temperatureB[i - 1] > 0)
|| (temperatureA[i] - temperatureA[i - 1] < 0 && temperatureB[i] - temperatureB[i - 1] < 0)
|| (temperatureA[i] - temperatureA[i - 1] == 0 && temperatureB[i] - temperatureB[i - 1] == 0)) {
isEqual[i] = true;
}
}
int max = 0;
int cnt = 0;
for (boolean eq : isEqual) {
if (eq) {
cnt++;
max = Math.max(max, cnt);
} else {
cnt = 0;
}
}
return max;
}
}T2. 交通枢纽(4 分)
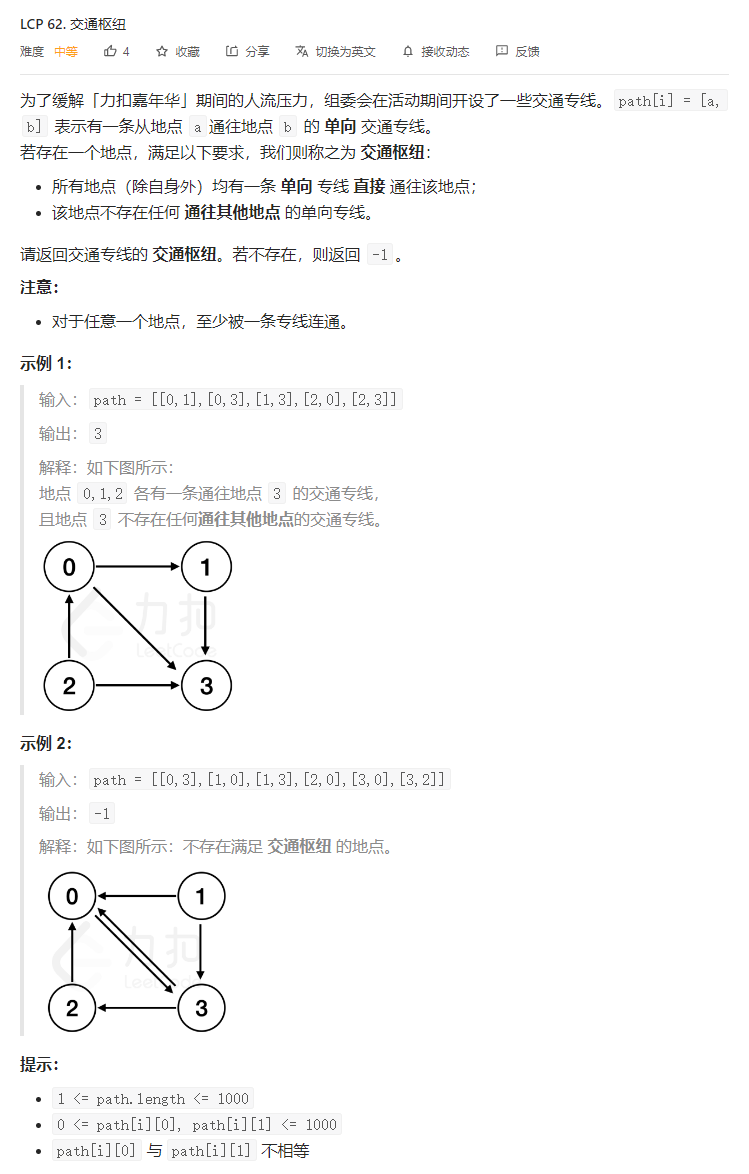
解题思路
图论。对每个节点计算入度和出度。交通枢纽即入度为 节点数-1 && 出度为 0 的节点。
时间复杂度:O(n+m)。
参考代码
class Solution {
public int transportationHub(int[][] path) {
Map<Integer, Integer> inDegrees = new HashMap<>();
Map<Integer, Integer> outDegrees = new HashMap<>();
// 出现过的节点
Set<Integer> seen = new HashSet<>();
for (int[] tuple : path) {
int u = tuple[0];
int v = tuple[1];
// v入度+1 u出度+1
inDegrees.put(v, inDegrees.getOrDefault(v, 0) + 1);
outDegrees.put(u, outDegrees.getOrDefault(u, 0) + 1);
seen.add(u);
seen.add(v);
}
// 入度为 n-1 && 出度为 0
int sz = seen.size();
for (int x : seen) {
if (inDegrees.getOrDefault(x, 0) == sz - 1 && outDegrees.getOrDefault(x, 0) == 0) {
return x;
}
}
return -1;
}
}T3. 弹珠游戏(6 分)

解题思路
BFS 模拟。本题疑似存在卡常,需从 '.' 到 'O',逆向的话会 TLE。
时间复杂度:O(nm)。
参考代码
class Solution {
// up left down right
private static final int[] DX = {-1, 0, 1, 0};
private static final int[] DY = {0, 1, 0, -1};
public int[][] ballGame(int num, String[] plate) {
int M = plate.length;
int N = plate[0].length();
char[][] chars = new char[M][N];
for (int i = 0; i < M; i++) {
chars[i] = plate[i].toCharArray();
}
// [startM, startN, curM, curN, dir]
Queue<int[]> queue = new LinkedList<>();
for (int j = 1; j < N - 1; j++) {
// 上边界往下走
if (chars[0][j] == '.') {
queue.add(new int[]{0, j, 0, j, 2});
}
// 下边界往上走
if (chars[M - 1][j] == '.') {
queue.add(new int[]{M - 1, j, M - 1, j, 0});
}
}
for (int i = 1; i < M - 1; i++) {
// 左边界往右走
if (chars[i][0] == '.') {
queue.add(new int[]{i, 0, i, 0, 1});
}
// 右边界往左走
if (chars[i][N - 1] == '.') {
queue.add(new int[]{i, N - 1, i, N - 1, 3});
}
}
List<int[]> resList = new ArrayList<>();
while (!queue.isEmpty() && num >= 0) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int[] tuple = queue.remove();
int startM = tuple[0];
int startN = tuple[1];
int curM = tuple[2];
int curN = tuple[3];
int dir = tuple[4];
if (chars[curM][curN] == 'O') {
resList.add(new int[]{startM, startN});
continue;
} else if (chars[curM][curN] == 'E') {
// "E" 表示顺时针转向器(弹珠经过时方向将顺时针旋转 90 度);
dir = (dir + 1) % 4;
} else if (chars[curM][curN] == 'W') {
// "W" 表示逆时针转向器(弹珠经过时方向将逆时针旋转 90 度);
dir = (dir + 3) % 4;
}
int nextM = curM + DX[dir];
int nextN = curN + DY[dir];
if (nextM >= 0 && nextM < M && nextN >= 0 && nextN < N) {
queue.add(new int[]{startM, startN, nextM, nextN, dir});
}
}
num--;
}
return resList.toArray(new int[resList.size()][]);
}
}T4. 二叉树灯饰(8 分)

解题思路
树形 DP。令 f(TreeNode node, boolean switch2Odd, boolean switch3) 表示当前节点,父节点 开关2 切换次数是否是奇数次,父节点 开关3 是否切换时,关闭子树所有灯最少需要操作多少次开关。
- 若当前节点为开灯状态,则
res = min(切换开关1, 切换开关2, 切换开关3, 切换开关123)。 - 若当前节点为关灯状态,则
res = min(不操作, 切换开关12, 切换开关13, 切换开关23)。
时间复杂度:O(n)。
参考代码
class Solution {
private Map<TreeNode, Map<Integer, Integer>> memo;
public int closeLampInTree(TreeNode root) {
memo = new HashMap<>();
return f(root, 0);
}
// f(TreeNode node, boolean switch2Odd, boolean switch3)
// 表示当前节点,父节点开关 2 切换次数是否是奇数次,父节点开关 3 是否切换时,关闭子树所有灯最少需要操作多少次开关
// f(node, 0/1, 0/1) => f(node, mask) 方便进行记忆化 mask = switch2Odd << 1 + switch3
private int f(TreeNode node, int mask) {
if (node == null) {
return 0;
}
// 记忆化搜索
if (memo.containsKey(node) && memo.get(node).containsKey(mask)) {
return memo.get(node).get(mask);
}
int res = Integer.MAX_VALUE;
int bit0 = mask & 1;
int bit1 = (mask >> 1) & 1;
// 灯 = 开,且 switch2_odd, switch3 抵消,最终还是开
// 灯 = 关,且 switch2_odd, switch3 不抵消,最终还是开
if ((node.val == 1) == (bit1 == bit0)) {
res = Math.min(res, f(node.left, bit1 << 1) + f(node.right, bit1 << 1) + 1);
res = Math.min(res, f(node.left, (1 - bit1) << 1) + f(node.right, (1 - bit1) << 1) + 1);
res = Math.min(res, f(node.left, (bit1 << 1) + 1) + f(node.right, (bit1 << 1) + 1) + 1);
res = Math.min(res, f(node.left, ((1 - bit1) << 1) + 1) + f(node.right, ((1 - bit1) << 1) + 1) + 3);
} else {
res = Math.min(res, f(node.left, bit1 << 1) + f(node.right, bit1 << 1));
res = Math.min(res, f(node.left, (1 - bit1) << 1) + f(node.right, (1 - bit1) << 1) + 2);
res = Math.min(res, f(node.left, (bit1 << 1) + 1) + f(node.right, (bit1 << 1) + 1) + 2);
res = Math.min(res, f(node.left, ((1 - bit1) << 1) + 1) + f(node.right, ((1 - bit1) << 1) + 1) + 2);
}
memo.computeIfAbsent(node, key -> new HashMap<>()).put(mask, res);
return res;
}
}T5. 舒适的湿度(10 分)
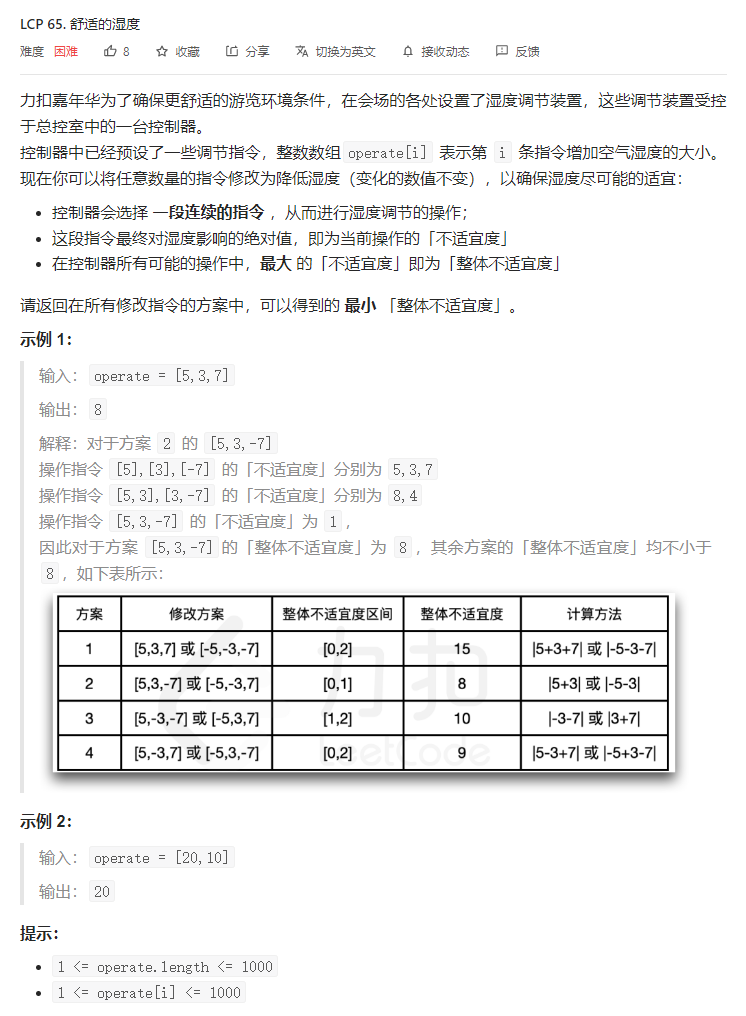
解题思路
CF 原题:https://codeforces.com/problemset/problem/1579/G 是 Div. 3 的最后一题,rating 分 2200。
动态规划。令 f[i][j] 表示前 i 个数,最右端点纵坐标与折线图最低端点纵坐标差值为 j 时,折线图最大最小值差值的最小值。
时间复杂度:O(n·max(operate[i]))。
参考代码
class Solution {
public int unSuitability(int[] operate) {
int len = operate.length;
// 答案显然不会超过最大 operate[i] 的 2 倍
int max = Arrays.stream(operate).max().orElseThrow() * 2 + 1;
// f[i][j] 表示前 i 个数,最右端点纵坐标与折线图最低端点纵坐标差值为 j 时,折线图最大最小值差值的最小值
int[][] f = new int[len + 1][max];
for (int i = 0; i < len + 1; i++) {
Arrays.fill(f[i], Integer.MAX_VALUE);
}
f[0][0] = 0;
for (int i = 0; i < len; i++) {
int x = operate[i];
for (int j = 0; j < max; j++) {
if (f[i][j] == Integer.MAX_VALUE) {
continue;
}
if (j + x < max) {
f[i + 1][j + x] = Math.min(f[i + 1][j + x], Math.max(f[i][j], j + x));
}
if (j >= x) {
f[i + 1][j - x] = Math.min(f[i + 1][j - x], f[i][j]);
} else {
f[i + 1][0] = Math.min(f[i + 1][0], f[i][j] - j + x);
}
}
}
return Arrays.stream(f[len]).min().orElseThrow();
}
}(全文完)