LCCUP'23 力扣杯春季编程大赛-战队赛/个人赛
2023年12月17日大约 12 分钟
LCCUP'23 力扣杯春季编程大赛-战队赛/个人赛
战队赛
比赛时间 2023-05-07。感谢队友 @kexp、@yuekunwang,喜提 Rank 84,超过了 97.8% 的选手!
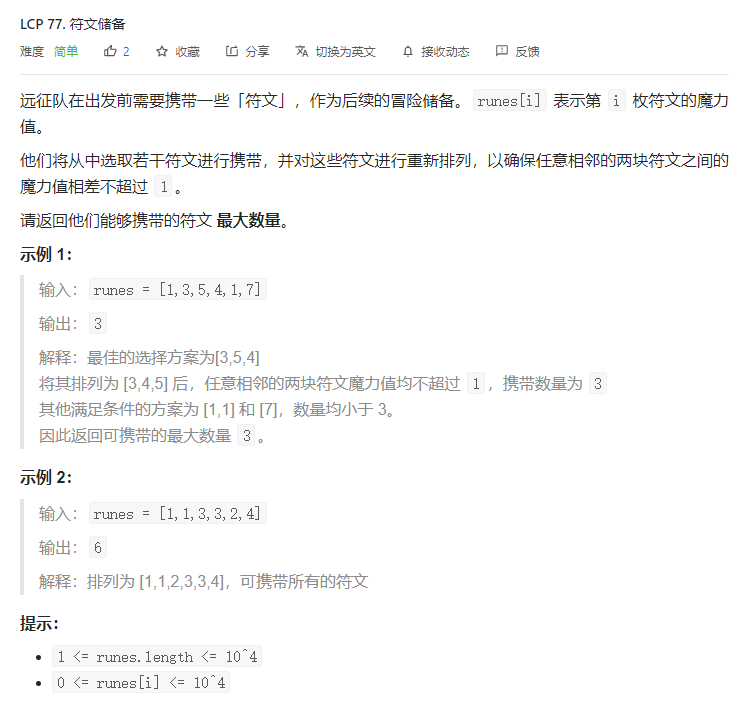
T1. 符文储备(2 分)
解题思路
观察到值域比较小,预处理每个数的频次,然后线性遍历取最大连续和即可。
时间复杂度:O(n)。
参考代码
class Solution {
private static final int MAX_N = (int) (1e4 + 5);
public int runeReserve(int[] runes) {
int[] cnt = new int[MAX_N];
for (int x : runes) {
cnt[x]++;
}
int sum = 0, max = 0;
for (int x = 0; x < MAX_N; x++) {
if (cnt[x] > 0) {
sum += cnt[x];
max = Math.max(max, sum);
} else {
sum = 0;
}
}
return max;
}
}T2. 城墙防线(4 分)

解题思路
结果显然具有单调性,二分答案即可。
时间复杂度:O(nlogn)。
参考代码
class Solution {
public int rampartDefensiveLine(int[][] rampart) {
int n = rampart.length;
// [1, n-2] 个城墙中,能膨胀的最小值(即为二分答案的上界)
int min = Integer.MAX_VALUE;
for (int i = 1; i < n - 1; i++) {
int l = rampart[i][0] - rampart[i - 1][1];
int r = rampart[i + 1][0] - rampart[i][1];
min = Math.min(min, l + r);
}
int left = 1;
int right = min + 1;
while (left < right) {
int mid = left + (right - left) / 2;
// 边界二分 F, F,..., F, [T, T,..., T]
// ----------------------^
if (!checkMid(rampart, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left - 1;
}
// 时间复杂度 O(n) 校验能否膨胀 mid 个长度
private boolean checkMid(int[][] rampart, int mid) {
int n = rampart.length;
// 上一个城墙膨胀的右端点
int last = rampart[0][1];
for (int i = 1; i < n - 1; i++) {
int l = rampart[i][0] - last;
// Math.max(0, mid - l) 为右侧膨胀距离,注意非负
last = rampart[i][1] + Math.max(0, mid - l);
if (last > rampart[i + 1][0]) {
return false;
}
}
return true;
}
}T3. 提取咒文(6 分)

解题思路
三维 BFS。
比赛时候想歪了,写成多个路径,途径多个中间点。最终 TLE。。
时间复杂度:O(mnl)。
参考代码
class Solution {
public static final int[][] DIRECTIONS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
public int extractMantra(String[] matrix, String mantra) {
int m = matrix.length;
int n = matrix[0].length();
int l = mantra.length();
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{0, 0, 0});
boolean[][][] visited = new boolean[m][n][l];
visited[0][0][0] = true;
int step = 1;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int[] tuple = queue.remove();
int cx = tuple[0], cy = tuple[1], cl = tuple[2];
// 可以提取
if (matrix[cx].charAt(cy) == mantra.charAt(cl)) {
if (cl == l - 1) {
return step;
}
if (!visited[cx][cy][cl + 1]) {
visited[cx][cy][cl + 1] = true;
queue.add(new int[]{cx, cy, cl + 1});
}
}
for (int[] dir : DIRECTIONS) {
int nx = cx + dir[0], ny = cy + dir[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
if (!visited[nx][ny][cl]) {
visited[nx][ny][cl] = true;
queue.add(new int[]{nx, ny, cl});
}
}
}
}
step++;
}
return -1;
}
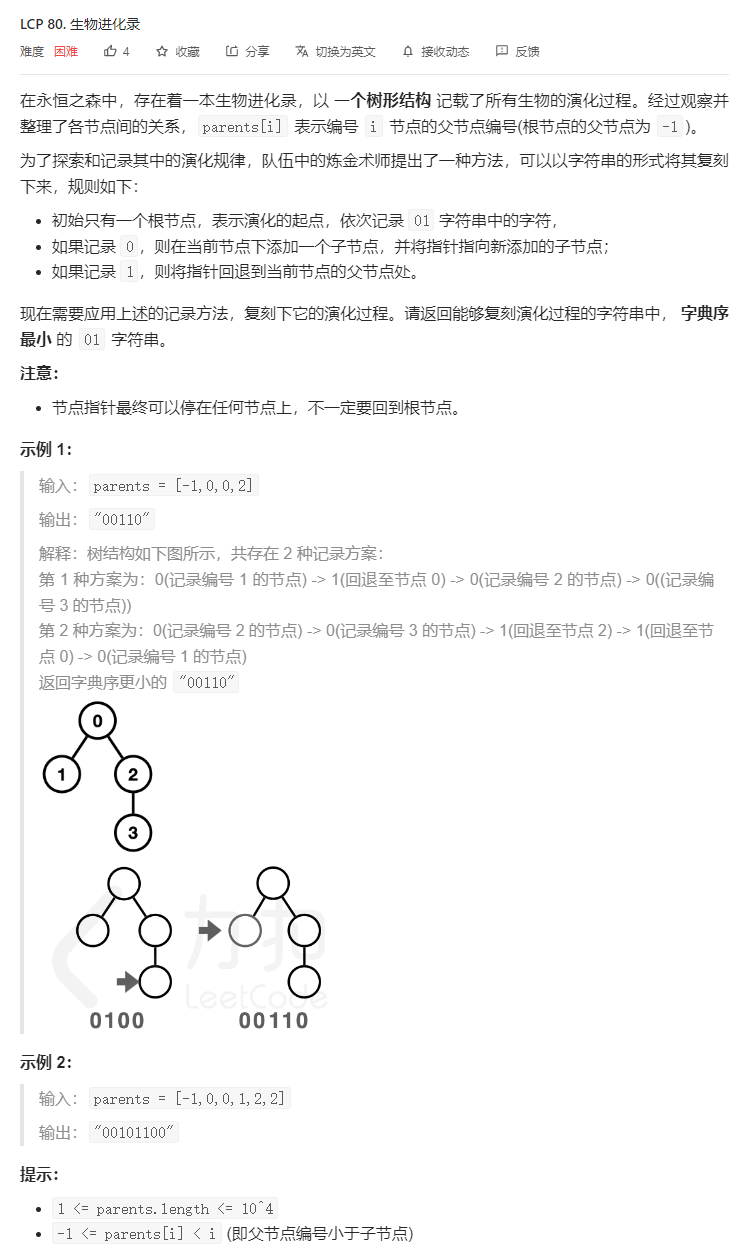
}T4. 生物进化录(8 分)
解题思路
树形 DP + 排序。
相似题目: 761. 特殊的二进制序列
时间复杂度:O(n^2)。
参考代码
class Solution {
private Map<Integer, List<Integer>> g;
public String evolutionaryRecord(int[] parents) {
int n = parents.length;
g = new HashMap<>();
for (int i = 1; i < n; i++) {
g.computeIfAbsent(parents[i], key -> new ArrayList<>()).add(i);
}
// 去掉第一个 0 和末尾连续的 1
return dfs(0).substring(1).replaceAll("1+$", "");
}
private String dfs(int x) {
List<String> a = new ArrayList<>();
for (int y : g.getOrDefault(x, new ArrayList<>())) {
a.add(dfs(y));
}
Collections.sort(a);
return "0" + String.join("", a) + "1";
}
}T5. 与非的谜题(9 分)

解题思路
暴力出奇迹。
正解应为:拆位 + 线段树。NAND 的性质:NAND 0 一定等于 1,NAND 1 相当于取反。
时间复杂度:O(能过)。
参考代码
class Solution {
private static int FULL;
public int getNandResult(int k, int[] arr, int[][] operations) {
FULL = (1 << k) - 1;
int res = 0;
for (int[] op : operations) {
int type = op[0], x = op[1], y = op[2];
if (type == 1) {
for (int ai : arr) y = nand(y, ai);
// 偶数次
if ((x & 1) == 0) {
for (int ai : arr) y = nand(y, ai);
}
res ^= y;
} else {
arr[x] = y;
}
}
return res;
}
private int nand(int a, int b) {
return ~(a & b) & FULL;
}
}T6. 万灵之树(10 分)

解题思路
宫万题解 https://leetcode.cn/problems/cnHoX6/solution/gong-mo-ti-jie-by-hqztrue-q5a0/
- 魔鬼数字
1996090921 = 11 * 17 * 17 * 293 * 2143;初步看是蛙佬手写 hash 时的专属数字; Function/BiFunction是 Java 的函数编程接口;- 扩展欧几里得法
(exgcd)求 逆元(inv); - 阶乘函数
(fac); - 组合函数
(C); ++T;的作用就是清空 哈希表(妙啊);
时间复杂度:O(能过)。
参考代码
class Solution {
private static final int N = 9, M0 = 205;
private final int[] pow10 = new int[M0], pinv = new int[M0], l = new int[N], len = new int[1 << N];
private int n, ans, p, r, B;
private final Map<Integer, List<Integer>> c = new HashMap<>();
private final Map<Integer, List<Node>> d = new HashMap<>();
private final Map<Integer, Integer> hash = new HashMap<>();
public int treeOfInfiniteSouls(int[] gem, int p, int target) {
n = gem.length;
ans = 0;
B = (n + 2) / 3;
this.p = p;
this.r = target;
if (p == 2 || p == 5) {
return p == 2 && target == 1 || p == 5 && target == 4 ? (int) (C((n - 1) * 2, n - 1) / n * fac(n)) : 0;
}
pow10[0] = 1 % p;
for (int i = 1; i < M0; ++i) {
pow10[i] = (int) ((long) pow10[i - 1] * 10 % p);
}
for (int i = 0; i < M0; ++i) {
pinv[i] = (int) inv(pow10[i], p);
}
for (int i = 0; i < n; ++i) {
l[i] = log10(gem[i]);
}
for (int i = 1; i < (1 << n); ++i) {
len[i] = (pop(i) * 2 - 1) * 2;
for (int j = 0; j < n; ++j) {
if ((i & (1 << j)) > 0) {
len[i] += l[j];
}
}
}
for (int i = 0; i < n; ++i) {
c.computeIfAbsent(1 << i, key -> new ArrayList<>()).add((int) (((long) gem[i] * 10 + pow10[l[i] + 1] + 9) % p));
}
for (int i = 1; i < (1 << n); ++i) {
if (pop(i) <= B * 2) { //component below u
int t = pow10[len[i] - 1] + 9;
for (int j = (i - 1) & i; j != 0; j = (j - 1) & i) {
if (n == 9 || pop(i) < Math.max((n + 1) / 2, 2)
|| Math.max(pop(j), pop(i - j)) <= Math.min(B, (n - 1) / 2)) {
for (Integer v1 : c.getOrDefault(j, new ArrayList<>())) {
long t1 = (long) v1 * pow10[len[i - j] + 1] + t;
for (Integer v2 : c.getOrDefault(i - j, new ArrayList<>())) {
c.computeIfAbsent(i, key -> new ArrayList<>()).add((int) (((long) v2 * 10 + t1) % p));
}
}
}
}
}
}
d.computeIfAbsent(1 << n, key -> new ArrayList<>()).add(new Node(0, 0, 0)); //component above u
BiFunction<Integer, Integer, Boolean> yes = (x, y) -> true;
BiFunction<Integer, Integer, Boolean> no = (x, y) -> false;
if (n == 9) {
calc(4, yes, no, (j) -> pop(j) != 6); //remove size 6
calc(5, (i, j) -> j != (1 << n) || pop(i - j) >= 2, //remove size 5
no, (j) -> pop(j) != 5);
calc(6, (i, j) -> j != (1 << n) || pop(i - j) == 3, //remove size 4
(i, j) -> j == (1 << n) && pop(i - j) == 4,
(j) -> pop(j) != 4);
} else {
calc(n / 2 + 1, yes,
(i, j) -> n % 2 == 0 && pop(j) == 1 && pop(i - j) == n / 2,
(j) -> pop(j) < (n + 1) / 2 || pop(j) > B * 2);
}
return ans;
}
private void calc(int t0, BiFunction<Integer, Integer, Boolean> f1,
BiFunction<Integer, Integer, Boolean> f2, Function<Integer, Boolean> f3) {
for (int i = (1 << n) + 1; i < (1 << (n + 1)); ++i) {
d.getOrDefault(i, new ArrayList<>()).clear();
}
for (int i = 1 << n; i < (1 << (n + 1)); ++i) {
if (pop(i) <= t0) {
boolean _f2;
for (int j = (i - 1) & i; (j >> n) > 0; j = (j - 1) & i) {
if ((_f2 = f2.apply(i, j)) || f1.apply(i, j)) {
for (Node t : d.getOrDefault(j, new ArrayList<>())) {
int l1 = len[j - (1 << n)] - t.l + 2 * (j > (1 << n) ? 1 : 0);
for (Integer v2 : c.getOrDefault(i - j, new ArrayList<>())) {
d.computeIfAbsent(i, key -> new ArrayList<>()).add(new Node((t.v1 + pow10[l1]) % p,
(int) (((long) t.v2 * pow10[len[i - j] + 1] + (long) v2 * 10 + 9) % p),
t.l + len[i - j] + 1));
if (!_f2) {
d.computeIfAbsent(i, key -> new ArrayList<>()).add(new Node(
(int) ((t.v1 + pow10[l1 + len[i - j]] + (long) v2 * pow10[l1]) % p),
(int) (((long) t.v2 * 10 + 9) % p), t.l + 1));
}
}
}
}
}
int j = (1 << (n + 1)) - 1 - i;
hash.clear();
if (f3.apply(j)) continue;
for (Integer v : c.getOrDefault(j, new ArrayList<>())) {
hash.put(v, hash.getOrDefault(v, 0) + 1);
}
for (Node t : d.getOrDefault(i, new ArrayList<>())) {
int i1 = (int) ((((long) r - t.v2 - (long) t.v1 * pow10[len[j] + t.l]) % p + p) * pinv[t.l] % p);
ans += hash.getOrDefault(i1, 0);
}
}
}
}
private static class Node {
int v1, v2, l;
public Node(int v1, int v2, int l) {
this.v1 = v1;
this.v2 = v2;
this.l = l;
}
}
private int pop(int x) {
return Integer.bitCount(x);
}
private int log10(int n) {
return n < 10 ? 1 : log10(n / 10) + 1;
}
private long inv(long a, long b) {
x = 0;
y = 0;
exgcd(a, b);
return (x % b + b) % b;
}
private long x, y;
private long exgcd(long a, long b) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
long d = exgcd(b, a % b);
long tmp = x;
x = y;
y = tmp - a / b * y;
return d;
}
private long fac(int n) {
long res = 1;
while (n > 0) res *= n--;
return res;
}
private long C(int n, int m) {
long res = 1L;
for (int i = 1; i <= m; i++) res = res * (n - i + 1) / i;
return res;
}
}个人赛
比赛时间 2023-04-22。历史上第四次参加个人赛,终于不是月末周六了。打破两题魔咒。。
T1. 补给马车(2 分)

解题思路
模拟。
时间复杂度:O(n^2)。
参考代码
class Solution {
private int halfN;
public int[] supplyWagon(int[] supplies) {
halfN = supplies.length / 2;
return dfs(supplies);
}
private int[] dfs(int[] cur) {
int n = cur.length;
if (n <= halfN) {
return cur;
}
int minI = 0;
int minSum = Integer.MAX_VALUE;
for (int i = 0; i + 1 < n; i++) {
if (minSum > cur[i] + cur[i + 1]) {
minSum = cur[i] + cur[i + 1];
minI = i;
}
}
int[] next = new int[n - 1];
for (int i = 0; i <= minI; i++) {
next[i] = cur[i];
}
for (int i = minI; i < n - 1; i++) {
next[i] += cur[i + 1];
}
return dfs(next);
}
}T2. 探险营地(4 分)

解题思路
模拟。
使用 HashSet,不同营地即为差值。
时间复杂度:O(|S|)。即所有字符串的长度之和。
参考代码
class Solution {
public int adventureCamp(String[] expeditions) {
int n = expeditions.length;
Set<String> set = new HashSet<>();
for (String s : expeditions[0].split("->")) {
// 营地的名称长度均大于 0。
if (s.length() > 0) {
set.add(s);
}
}
int maxI = -1;
int maxCnt = 0;
for (int i = 1; i < n; i++) {
Set<String> tmp = new HashSet<>();
for (String s : expeditions[i].split("->")) {
if (s.length() > 0) {
tmp.add(s);
}
}
tmp.removeAll(set);
int cnt = tmp.size();
set.addAll(tmp);
if (maxCnt < cnt) {
maxCnt = cnt;
maxI = i;
}
}
return maxI;
}
}T3. 最强祝福力场(6 分)

解题思路
离散化 + 二维差分。
时间复杂度:O(n^2)。
参考代码
class Solution {
public int fieldOfGreatestBlessing(int[][] forceField) {
// 离散化 begin
Set<Double> xSet = new HashSet<>();
Set<Double> ySet = new HashSet<>();
for (int[] fo : forceField) {
double x1 = fo[0] + fo[2] / 2.0, y1 = fo[1] + fo[2] / 2.0;
double x2 = fo[0] - fo[2] / 2.0, y2 = fo[1] - fo[2] / 2.0;
xSet.add(x1);
xSet.add(x2);
ySet.add(y1);
ySet.add(y2);
}
int xsz = xSet.size();
double[] xArr = new double[xsz];
int id = 0;
for (double x : xSet) {
xArr[id++] = x;
}
Arrays.sort(xArr);
int ysz = ySet.size();
double[] yArr = new double[ysz];
id = 0;
for (double x : ySet) {
yArr[id++] = x;
}
Arrays.sort(yArr);
// 离散化 end
PrefixSum2d prefixSum2d = new PrefixSum2d(new int[xsz][ysz]);
for (int[] fo : forceField) {
double x1 = fo[0] + fo[2] / 2.0, y1 = fo[1] + fo[2] / 2.0;
double x2 = fo[0] - fo[2] / 2.0, y2 = fo[1] - fo[2] / 2.0;
int x1id = getId(xArr, x1), x2id = getId(xArr, x2);
int y1id = getId(yArr, y1), y2id = getId(yArr, y2);
prefixSum2d.rangeAdd(x2id, y2id, x1id, y1id, 1);
}
int max = 0;
// 原数组
int[][] originArr = prefixSum2d.originalArray();
for (int i = 0; i < xsz; i++) {
for (int j = 0; j < ysz; j++) {
max = Math.max(max, originArr[i][j]);
}
}
return max;
}
private int getId(double[] yArr, double x) {
return Arrays.binarySearch(yArr, x);
}
private static class PrefixSum2d {
private final int M;
private final int N;
private final int[][] preSum2d;
private final int[][] diff2d;
public PrefixSum2d(int[][] matrix) {
this.M = matrix.length;
this.N = matrix[0].length;
// 预处理前缀和
preSum2d = new int[M + 1][N + 1];
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
// 当前格 = 上 + 左 - 左上 + 原值
preSum2d[i][j] = preSum2d[i - 1][j] + preSum2d[i][j - 1] - preSum2d[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
// 差分 init
diff2d = new int[M + 1][N + 1];
}
// 二维前缀和:求 matrix [row1,col1] 到 [row2,col2] 的累加和
public int sumRegion(int row1, int col1, int row2, int col2) {
return preSum2d[row2 + 1][col2 + 1] - preSum2d[row2 + 1][col1] - preSum2d[row1][col2 + 1] + preSum2d[row1][col1];
}
// 二维差分:matrix [row1,col1] 到 [row2,col2] 全部增加 inc
public void rangeAdd(int row1, int col1, int row2, int col2, int inc) {
diff2d[row1][col1] += inc;
diff2d[row1][col2 + 1] -= inc;
diff2d[row2 + 1][col1] -= inc;
diff2d[row2 + 1][col2 + 1] += inc;
}
// 二维差分:获取原数组
public int[][] originalArray() {
int[][] res = new int[M][N];
// 0 行
res[0][0] = diff2d[0][0];
for (int j = 1; j < N; j++) {
res[0][j] = res[0][j - 1] + diff2d[0][j];
}
// 0 列
for (int i = 1; i < M; i++) {
res[i][0] = res[i - 1][0] + diff2d[i][0];
}
// 1 行 1 列。。。
for (int i = 1; i < M; i++) {
for (int j = 1; j < N; j++) {
res[i][j] = res[i - 1][j] + res[i][j - 1] - res[i - 1][j - 1] + diff2d[i][j];
}
}
return res;
}
}
}T4. 传送卷轴(8 分)

解题思路
BFS + 二分答案。
时间复杂度:O(mnlog(mn))。
参考代码
class Solution {
private static final int INF = (int) 1e9;
private static final int[][] DIRECTIONS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
private char[][] grid;
private int n;
private int[][] dist;
public int challengeOfTheKeeper(String[] maze) {
this.n = maze.length;
grid = new char[n][n];
for (int i = 0; i < n; i++) {
grid[i] = maze[i].toCharArray();
}
int sx = 0, sy = 0, tx = 0, ty = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
char ch = grid[i][j];
if (ch == 'S') {
sx = i;
sy = j;
} else if (ch == 'T') {
tx = i;
ty = j;
}
}
}
// BFS 求终点到其余点的最短路
dist = new int[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(dist[i], INF);
}
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{tx, ty, 0});
boolean[][] visited = new boolean[n][n];
visited[tx][ty] = true;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int[] tuple = queue.remove();
int cx = tuple[0], cy = tuple[1], cstep = tuple[2];
dist[cx][cy] = cstep;
for (int[] dir : DIRECTIONS) {
int nx = cx + dir[0];
int ny = cy + dir[1];
if (nx >= 0 && nx < n && ny >= 0 && ny < n && !visited[nx][ny] && grid[nx][ny] != '#') {
visited[nx][ny] = true;
queue.add(new int[]{nx, ny, cstep + 1});
}
}
}
}
// 无法从 S 到 T
if (dist[sx][sy] == INF) {
return -1;
}
// 二分答案
// 走到一个位置(陷阱),传送之后还需要走 > mid 步
// 如果在不走 # 不走陷阱的情况下,可以到达终点 => 答案 <= mid
// 如果无法到达终点 => 答案 > mid
int left = 0;
int right = n * n;
while (left < right) {
int mid = left + (right - left) / 2;
// 边界二分 F, F,..., F, [T, T,..., T]
// ----------------------^
if (checkMid(sx, sy, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left == n * n ? -1 : left;
}
private boolean checkMid(int sx, int sy, int mid) {
boolean[][] vis = new boolean[n][n];
return dfs(vis, sx, sy, mid);
}
private boolean dfs(boolean[][] vis, int i, int j, int mid) {
if (i >= 0 && i < n && j >= 0 && j < n && !vis[i][j] && grid[i][j] != '#') {
if (grid[i][j] == 'T') {
return true;
}
vis[i][j] = true;
if (grid[i][j] == '.') {
if (grid[i][n - 1 - j] != '#' && dist[i][n - 1 - j] > mid) {
return false;
}
if (grid[n - 1 - i][j] != '#' && dist[n - 1 - i][j] > mid) {
return false;
}
}
for (int[] dir : DIRECTIONS) {
int nx = i + dir[0];
int ny = j + dir[1];
if (dfs(vis, nx, ny, mid)) {
return true;
}
}
}
return false;
}
}T5. 魔法棋盘(10 分)
解题思路
自动机 + 状态压缩 + 记忆化搜索
https://leetcode.cn/problems/1ybDKD/solution/zhuang-ya-dp-bao-sou-xia-yi-ge-zhuang-ta-9dad/
- 时间复杂度:
O(n·21^m)。在全为?的情况下,dfs 最多调用5601518次。 - 空间复杂度:
O(n·8^m)。
参考代码
class SolutionLCP76 {
private static final int[][] TRANS = {
// (填 B 之后的状态,填 R 之后的状态)
// 0. 空
// 1. 一个 B
// 2. 一个 R
// 3. 连续多个 B
// 4. 连续多个 R
// 5. BR 交替,且以 B 结尾
// 6. BR 交替,且以 R 结尾
{1, 2},
{3, 6},
{5, 4},
{3, -1},
{-1, 4},
{-1, 6},
{5, -1},
};
private int n, m;
private char[][] board;
private long[][] memo;
public long getSchemeCount(int n, int m, String[] chessboard) {
// 1 <= n*m <= 30 意味着什么?在旋转后,保证列数 m <= 5
// 用 3 个比特表示 7 个状态
// 所有列的状态组合起来 pow(7, m) 个状态 => 状态压缩
// 每一排从左到右增量去构造 ? => 留空/B/R
this.n = n;
this.m = m;
this.board = strings2chars2(chessboard);
if (n < m) {
this.n = m;
this.m = n;
this.board = rotate(board);
}
memo = new long[this.n + 1][1 << (this.m * 3)];
for (int i = 0; i < this.n + 1; i++) {
Arrays.fill(memo[i], -1);
}
return dfs(0, 0);
}
private char[][] strings2chars2(String[] strs) {
int n = strs.length;
int m = strs[0].length();
char[][] res = new char[n][m];
for (int i = 0; i < n; i++) {
res[i] = strs[i].toCharArray();
}
return res;
}
// 行列转换
private char[][] rotate(char[][] board) {
int n = board.length;
int m = board[0].length;
char[][] res = new char[m][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
res[j][i] = board[i][j];
}
}
return res;
}
private long dfs(int r, int mask) {
if (memo[r][mask] != -1) {
return memo[r][mask];
}
if (r == n) {
return 1;
}
long res = dfs(r, 0, 0, mask);
memo[r][mask] = res;
return res;
}
private long dfs(int r, int c, int rowMask, int colMask) {
if (c == m) {
return dfs(r + 1, colMask);
}
char b = board[r][c];
if (b == 'B') {
return nxt(r, c, rowMask, colMask, 0);
} else if (b == 'R') {
return nxt(r, c, rowMask, colMask, 1);
} else if (b == '.') {
return dfs(r, c + 1, rowMask, colMask);
} else {
return nxt(r, c, rowMask, colMask, 0)
+ nxt(r, c, rowMask, colMask, 1)
+ dfs(r, c + 1, rowMask, colMask);
}
}
// (r,c) 填充颜色 color,判断是否合法
// 如果合法,就生成新的 rowMask 和 colMask
private long nxt(int r, int c, int rowMask, int colMask, int color) {
// 新的 rowMask
int rm = TRANS[rowMask][color];
if (rm < 0) {
return 0;
}
int c3 = c * 3;
// 新的 colMask 的第 c 列
int cm = TRANS[(colMask >> c3) & 7][color];
if (cm < 0) {
return 0;
}
// 修改 colMask 的第 c 列
cm = colMask & ~(7 << c3) | (cm << c3);
return dfs(r, c + 1, rm, cm);
}
}(全文完)